estimada,
Sobre la derivada del vector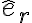 : de acuero con el dibujo que adjuntaste, la velocidad angular es entrente al dibujo (osea según
: de acuero con el dibujo que adjuntaste, la velocidad angular es entrente al dibujo (osea según 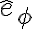 ). Entonces según la regla de la mano derecha:
). Entonces según la regla de la mano derecha: 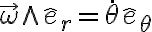
No veo en tu dibujo los vectores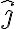 y
y 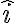 pero en función de los versores que están ahí la descomposición queda:
pero en función de los versores que están ahí la descomposición queda:
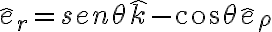
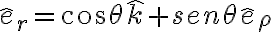
Probá con los vectores descompuestos de esta manera.
Saludos
Sobre la derivada del vector
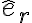 : de acuero con el dibujo que adjuntaste, la velocidad angular es entrente al dibujo (osea según
: de acuero con el dibujo que adjuntaste, la velocidad angular es entrente al dibujo (osea según 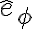 ). Entonces según la regla de la mano derecha:
). Entonces según la regla de la mano derecha: 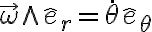
No veo en tu dibujo los vectores
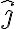 y
y 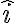 pero en función de los versores que están ahí la descomposición queda:
pero en función de los versores que están ahí la descomposición queda: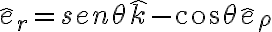
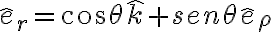
Probá con los vectores descompuestos de esta manera.
Saludos
