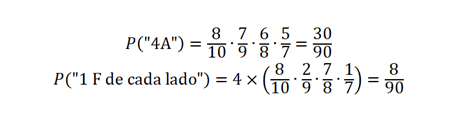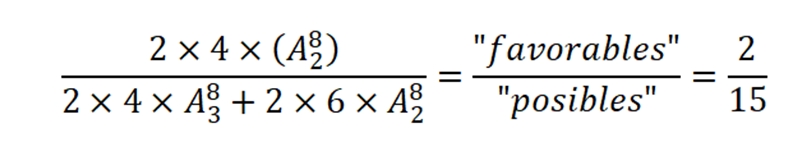Primer Parcial 2019 - Semestre Impar ejercicio 11

Primer Parcial 2019 - Semestre Impar ejercicio 11

de Thiago Caetano Acuña Vinoles -
Número de respuestas: 10

Buenas, no logro dar con el resultado. Quisiera saber si mi razonamiento está bien.

\( P(las\ cuatro\ monedas\ seleccionadas\ sean\ autenticas|el\ peso\ combinado\ de\ ambos\ pares\ es\ igual) =\\ \frac{P(las\ cuatro\ monedas\ autenticas\ y\ el\ peso...)}{P(el\ peso\ combinado\ de\ ambos\ pares\ es\ igual)} = \frac{P(las\ cuatro\ autenticas)}{P(el\ peso\ combinado\ de\ ambos\ pares\ es\ igual)} \)

Para \( P(las\ cuatro\ autenticas) \) hay solo una opción: se seleccionan dos auténticas y luego otras dos auténticas.  \( P(las\ cuatro\ autenticas) =\frac{8}{10} \frac{7}{9}\frac{6}{8}\frac{5}{7} =\frac{1}{3} \)

Y para \(P(el\ peso\ combinado\ de\ ambos\ pares\ es\ igual) \) hay 2 opciones: seleccionando una auténtica y una falsa en primera instancia y lo mismo luego o seleccionando las 4 auténticas.
Haciendo el diagrama de árbol me da \(P(el\ peso\ combinado\ de\ ambos\ pares\ es\ igual) =\frac{2}{5}\)

Luego \(P(las\ cuatro\ monedas\ seleccionadas\ sean\ autenticas|el\ peso\ combinado\ de\ ambos\ pares\ es\ igual)= \frac{\frac{1}{3} }{\frac{2}{5}} = \frac{5}{6} \)
En respuesta a Thiago Caetano Acuña Vinoles

Re: Primer Parcial 2019 - Semestre Impar ejercicio 11

de Eduardo Canale -
Hola Thiago, lo que pasa que para que el "peso combinado de ambos pares sea igual" puede ser que las cuatro sean autenticas o que los pares sean (A,F) y (A,F) o sea, una autentica y una falsificada en cada par.
Saludos
En respuesta a Eduardo Canale

Re: Primer Parcial 2019 - Semestre Impar ejercicio 11

de Thiago Caetano Acuña Vinoles -
Hola Eduardo, gracias por la respuesta.
Sin embargo, eso fue lo que dije (y lo que hice): "Y para P(el peso combinado de ambos pares es igual) hay 2 opciones: seleccionando una auténtica y una falsa en primera instancia y lo mismo luego o seleccionando las 4 auténticas.".

En respuesta a Thiago Caetano Acuña Vinoles

Re: Primer Parcial 2019 - Semestre Impar ejercicio 11

de Andres Haroutunian Loffredo -

Buen día Thiago!

Pudiste resolver!?

Te paso el diagrama de árbol que me queda:


están las "4 auténticas" y " 1 falsa de cada lado"....el resultado es 19/45....

Saludos...

En respuesta a Andres Haroutunian Loffredo

Re: Primer Parcial 2019 - Semestre Impar ejercicio 11

de Thiago Caetano Acuña Vinoles -
Buen día Andres, no puede hacerlo no.
De todas formas, el resultado (según dice la solución del parcial) es \( \frac{15}{17}\), no \( \frac{19}{45}\).

Edit: Ya pude hacerlo. Mi error estaba en que consideraba sacar una verdadera y una falsa en el primer par y lo mismo para el segundo par como eventos independientes. 
Es decir, calculé la probabilidad de sacar una verdadera y una falsa en el primer par + la probabilidad de sacar una verdadera y una falsa en el segundo par en vez de calcular la probabilidad de sacar una verdadera y una falsa en el primer par intersección sacar una verdadera y una falsa en el segundo par.
En respuesta a Eduardo Canale

Re: Primer Parcial 2019 - Semestre Impar ejercicio 11

de Ezequiel Humberto Velazquez Manzor -
Buenas!, creo que entendí la forma de encarar el ejercicio que tuvieron. La forma que yo tome fue elegir la formula de bayes y definir 2 conjuntos Bi para siendo B1 las monedas son autenticas y B2 las monedas no lo son. y me quedo algo así  :




No se bien en que estoy fallando dado que para mi estoy cubriendo bien todos los casos de todas maneras
\( P(seanAutenticas | pesanIgual ) = 5/9 \) usando mi metodo.

Saludos y desde ya Muchas gracias!
En respuesta a Ezequiel Humberto Velazquez Manzor

Re: Primer Parcial 2019 - Semestre Impar ejercicio 11

de Andres Haroutunian Loffredo -
Ezequiel buen día!

Como llegaste al 5/9??? el denominador te da 19/45....y ahí tenés el resutlado...

Saludos....
En respuesta a Andres Haroutunian Loffredo

Re: Primer Parcial 2019 - Semestre Impar ejercicio 11

de Ezequiel Humberto Velazquez Manzor -
Buenas Andres, a ese resultado llego usando la formual de bayes. 

En el numerador tengo:

\( P(peso igual | sean autenticas) \cdot P(sean autenticas) = 1 \cdot 1/3 \)

 luego en el denominador tengo:

\( \sum_i{P(pesoigual | B_i)} = P(peso igual | sean autenticas)P(sean autenticas) + P(peso igual | no sean autenticas)P(no sean autenticas) = 1 \cdot1/3 + 2/3 \cdot 2/5 \)

y en un global la cuenta queda.

\( P(sean autenticas | peso igual) = \frac{1 \cdot1/3 }{1 \cdot1/3 + 2/3 \cdot2/5 } = \frac{5}{9} \)

Y asi es como llego,
Saludos!
En respuesta a Ezequiel Humberto Velazquez Manzor

Re: Primer Parcial 2019 - Semestre Impar ejercicio 11

de Andres Haroutunian Loffredo -

Ezequiel!

Sabes que lo que no funciona es el "4/10" !!! Esos serían los "esquemas posibles de configuración", pero cada uno de ellos hay que completarlos. Por ejemplo, si tenés una moneda falsa en la cuaterna, puedo completar las 3 restantes seleccionando dentro de las 8 auténticas, y tengo 4 esquemas posibles para ésta configuración, que es el dibujo tuyo. Y así con el resto... en resumen:


Miralo y comentame si estás de acuerdo... ahora aparece el 19/45...

Espero haber sido claro...

Saludos...

(Obs. Los " 2 " que aparecen multiplicando en la fracción tienen que ver con la moneda falsa...los 2 casos posibles cuando hay una sola, y el orden cuando están las dos)