Buenas tardes,
Me quedo una duda con el ejemplo 1 que se dio en las diapositivas adjuntas a este practico.
Se pide que 
Pero lo que noto es que para poder construir el autómata, en cierto punto asumimos que una de las dos tiras tuvo que haber terminado. Con eso me refiero a que el autómata presentado como solución, para poder procesar la 'c' de la 2º tira, se asegura que primero haya sido leída la 'b' (que puede estar o no) en el "final" de la 1º tira.
Por lo tanto, se podría tomar el par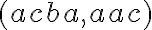 
y el mismo funciona en el autómata, ya que en realidad quedan mas cosas a recorrer luego de la 'b' de la primera tira. Ademas no se me ocurre como solucionar este problema, ya que si queremos poner un estado entre q4 y q5 donde se pueda leer la 1º tira, con el fin de ver si en realidad queda algo mas para leer de esa tira, podria pasar que no quede nada mas para leer, pero como ese estado intermedio solo lo puede ser recorrido por la tira 1, aunque haya mas cosas en la tira 2, queda trancada.
¿Se puede solucionar ese problema? EN caso de ser así, ¿que se podría hacer en este caso?
Saludos y gracias
Daniel