Hola, quería preguntar por la solución planteada del ejercicio en el practico 6 del curso del 2021, porque no entendí la justificación del problema. Gracias.
Recordás el teorema de los ceros? El mismo tiene un corolario inmediato que dice que si tenés dos funciones holomorfas 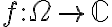 y
y 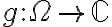 con
con 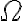 abierto y conexo, y tal que el conjunto
abierto y conexo, y tal que el conjunto 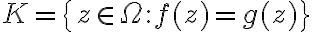 tiene un punto de acumulación en
tiene un punto de acumulación en 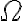 entonces al final la función
entonces al final la función  y
y  son iguales, es decir,
son iguales, es decir, 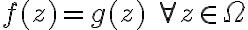 (es decir, al final
(es decir, al final 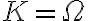 ).
).
Nota que el conjunto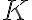 es el conjunto de puntos donde las funciones son iguales. Lo que esta diciendo el párrafo anterior es que si el conjunto
es el conjunto de puntos donde las funciones son iguales. Lo que esta diciendo el párrafo anterior es que si el conjunto 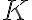 "es grande en
"es grande en 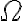 " entonces al final es todo
" entonces al final es todo 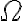 .
.
Volviendo al ejercicio, en este caso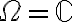 y
y 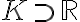 . Como
. Como 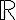 tiene un punto de acumulación en
tiene un punto de acumulación en 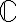 entonces cualquiera dos funciones que coincidan en
entonces cualquiera dos funciones que coincidan en 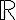 al final son iguales! y por lo tanto hay una sola función que valga
al final son iguales! y por lo tanto hay una sola función que valga 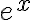 en el eje real.
en el eje real.
Contame si quedo un poco más claro, sino le buscamos otras palabras.
Saludos
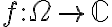 y
y 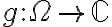 con
con 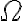 abierto y conexo, y tal que el conjunto
abierto y conexo, y tal que el conjunto 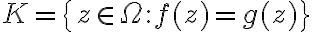 tiene un punto de acumulación en
tiene un punto de acumulación en 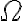 entonces al final la función
entonces al final la función  y
y  son iguales, es decir,
son iguales, es decir, 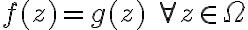 (es decir, al final
(es decir, al final 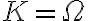 ).
).Nota que el conjunto
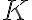 es el conjunto de puntos donde las funciones son iguales. Lo que esta diciendo el párrafo anterior es que si el conjunto
es el conjunto de puntos donde las funciones son iguales. Lo que esta diciendo el párrafo anterior es que si el conjunto 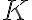 "es grande en
"es grande en 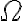 " entonces al final es todo
" entonces al final es todo 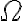 .
.Volviendo al ejercicio, en este caso
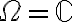 y
y 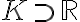 . Como
. Como 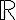 tiene un punto de acumulación en
tiene un punto de acumulación en 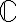 entonces cualquiera dos funciones que coincidan en
entonces cualquiera dos funciones que coincidan en 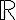 al final son iguales! y por lo tanto hay una sola función que valga
al final son iguales! y por lo tanto hay una sola función que valga 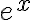 en el eje real.
en el eje real. Contame si quedo un poco más claro, sino le buscamos otras palabras.
Saludos
Se entendio, muchas gracias
