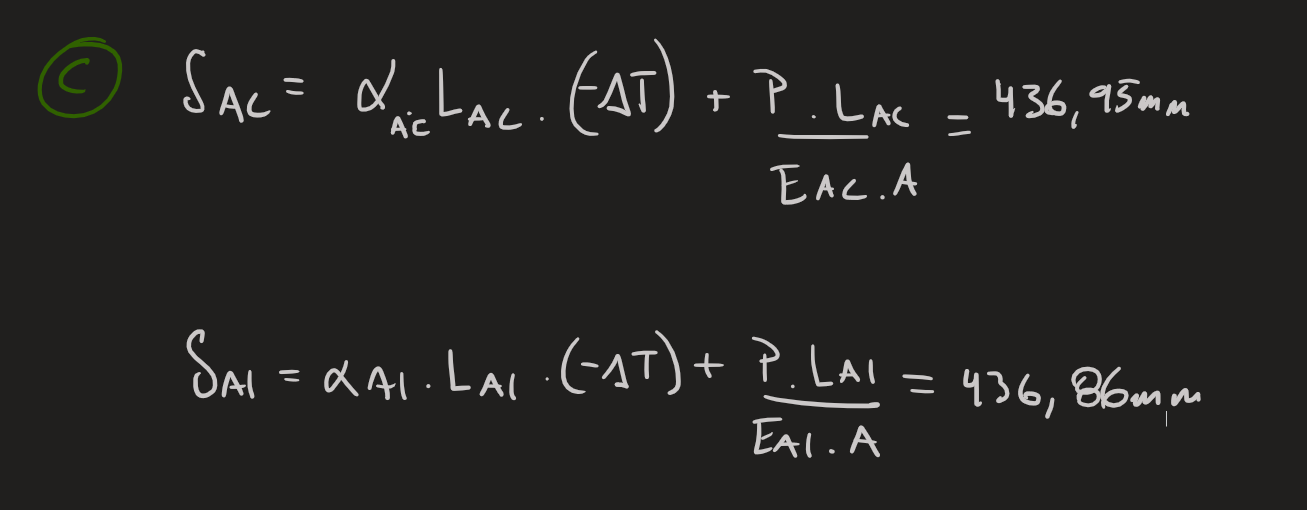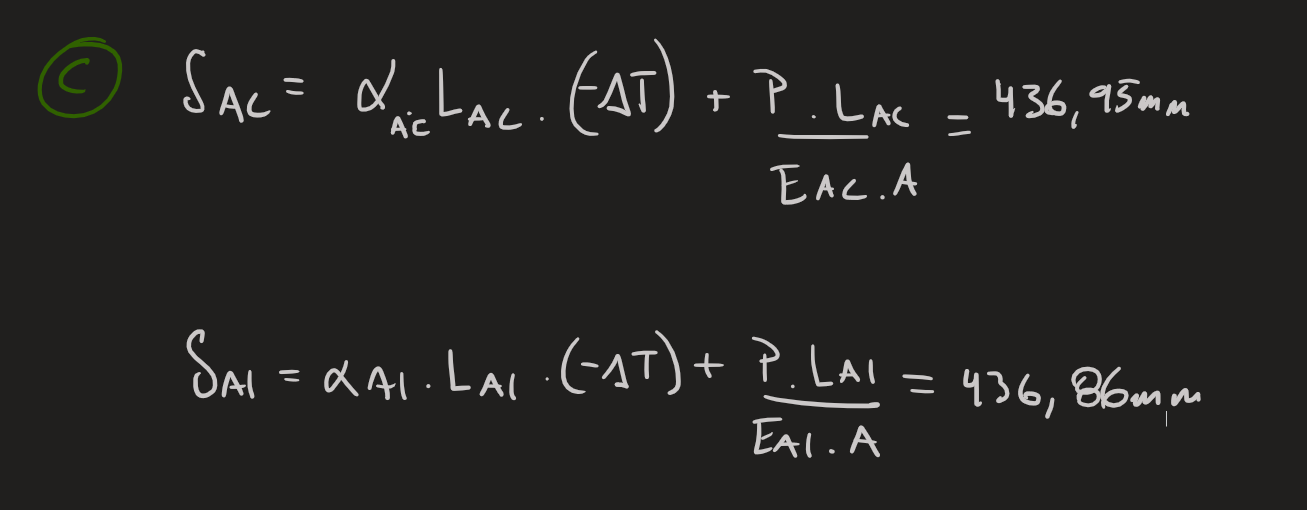Daniel,
Observando lo que planteas en la parte C, tengo varios comentarios:
1) Un aumento de temperatura debe provocar un estiramiento de la barra, por lo que el signo negativo para el ΔT en ambas ecuaciones no es coherente.
2) El estiramiento al que llegas es de 1/2 metro en una barra de 2 metros (demasiado estiramiento), por lo que me animo a decir que tiene que haber algún error en las unidades de los valores que estás utilizando.
3) Si sumo esto último, al comentario que haces de que "la elongación que agrega la temperatura no hace casi diferencia", es muy probable que la parte B y tal vez la parte A, también tenga el mismo problema de unidades.
Por las dudas, agrego el comentario siguiente que quizás el error puede venir por este lado:
La deformación ε suele ser adimensionada, dado que es el cociente de dos distancias. No obstante, si el numerador y el denominador están en las mismas unidades (por ejemplo: metros) este valor suele ser muy chico (por ejemplo: 0,002). Entonces por comodidad existes casos en los que el numerador y el denominador se colocan en diferentes unidades para que el resultado quede más amigable a la vista, por ejemplo 0,002 = 0,002m/1m podría escribirse como: 2mm/1m y terminaría siendo ε = 2 mm/m.
--> En el caso del ejercicio la deformación es ε = 873 μm/m, ( 1 μm = 10^(-6) m) ----> ε = 0.000873 m/m
Espero haya ayudado, sino lo vemos en clase.