Hola! Quería consultar si me podían confirmar que la propiedad escrita al final de la clase 09 (relacionada con una aproximación de la delta de dirac en continua) no tiene ningún error. Si es así, no la termino de entender. Me lo podrían explicar? Gracias.
Tengo la misma duda, traté de hacer la TdF de la función que plantea en el video y no me da un pulso de altura 1.
Hola. No sé si entendí exactamente su duda.
La transformada de el sinc del video, resulta en un pulso de altura uno (ver tabla de fórmulas). La forma más sencillo de probarlo, es utilizando el resultado del pulso en el tiempo (sinc en frecuencia) y la propiedad de dualidad. Si tienen alguna duda acerca de eso, pasen por alguna clase de consulta.
Luego, si la duda es la aproximación del sinc a la delta: no es trivial, así que es razonable que ocurran dudas. Existe una propiedad que NO demostraremos que básicamente dice que si una sucesión de funciones (como el sinc al varias tau) cumple que 1. su área es la misma para todos los elementos de la sucesión. 2 la sucesión de funciones converge uniformemente a cero fuera de cualquier abierto que incluya al cero (es decir, se va a cero salvo en 0), entonces esa sucesión converge a la delta multiplicada por el área.
Eso mismo es lo que le pasa a aquel rectángulo que se comenta en el vídeo y que ya vieron que converge a la delta.
Espero esto aclare las dudas.
Saludos
La transformada de el sinc del video, resulta en un pulso de altura uno (ver tabla de fórmulas). La forma más sencillo de probarlo, es utilizando el resultado del pulso en el tiempo (sinc en frecuencia) y la propiedad de dualidad. Si tienen alguna duda acerca de eso, pasen por alguna clase de consulta.
Luego, si la duda es la aproximación del sinc a la delta: no es trivial, así que es razonable que ocurran dudas. Existe una propiedad que NO demostraremos que básicamente dice que si una sucesión de funciones (como el sinc al varias tau) cumple que 1. su área es la misma para todos los elementos de la sucesión. 2 la sucesión de funciones converge uniformemente a cero fuera de cualquier abierto que incluya al cero (es decir, se va a cero salvo en 0), entonces esa sucesión converge a la delta multiplicada por el área.
Eso mismo es lo que le pasa a aquel rectángulo que se comenta en el vídeo y que ya vieron que converge a la delta.
Espero esto aclare las dudas.
Saludos
Hola, me mencionaron en el práctico sobre este error que aparece en el video de teórico [[Video] Transformada de Fourier de variable continua 2] "seys2022 - clase09" en el tiempo 2:07:13.
En el video se muestra como una "Propiedad" que la transformada de Fourier de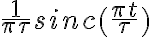
es un pulso rectangular de altura uno, que va desde 
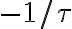a 
.
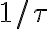En realidad, ese pulso es la transformada de Fourier de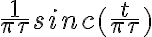
. A pesar del error en la expresión, sigue siendo válido lo explicado en el video que es que cuando 
tiende a cero, en el dominio de las frecuencias se tiene la función constante de altura uno y en el dominio del tiempo se tiene una función que tiende a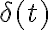 
.
Asimismo el error aparece también en la expresión que aparece en la siguiente "Propiedad" con la que culmina la clase.
Saludos,
Pablo
En el video se muestra como una "Propiedad" que la transformada de Fourier de
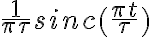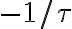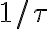es un pulso rectangular de altura uno, que va desde a .En realidad, ese pulso es la transformada de Fourier de
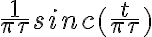. A pesar del error en la expresión, sigue siendo válido lo explicado en el video que es que cuando tiende a cero, en el dominio de las frecuencias se tiene la función constante de altura uno y en el dominio del tiempo se tiene una función que tiende a 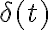.Asimismo el error aparece también en la expresión que aparece en la siguiente "Propiedad" con la que culmina la clase.
Saludos,
Pablo
Era eso, muchas gracias!
Hola! La única duda que me quedó al respecto es la siguiente: en la imágen se puede ver como el área dentro de esa figura que "aproxima" a delta es 2, cuando debería ser 1.
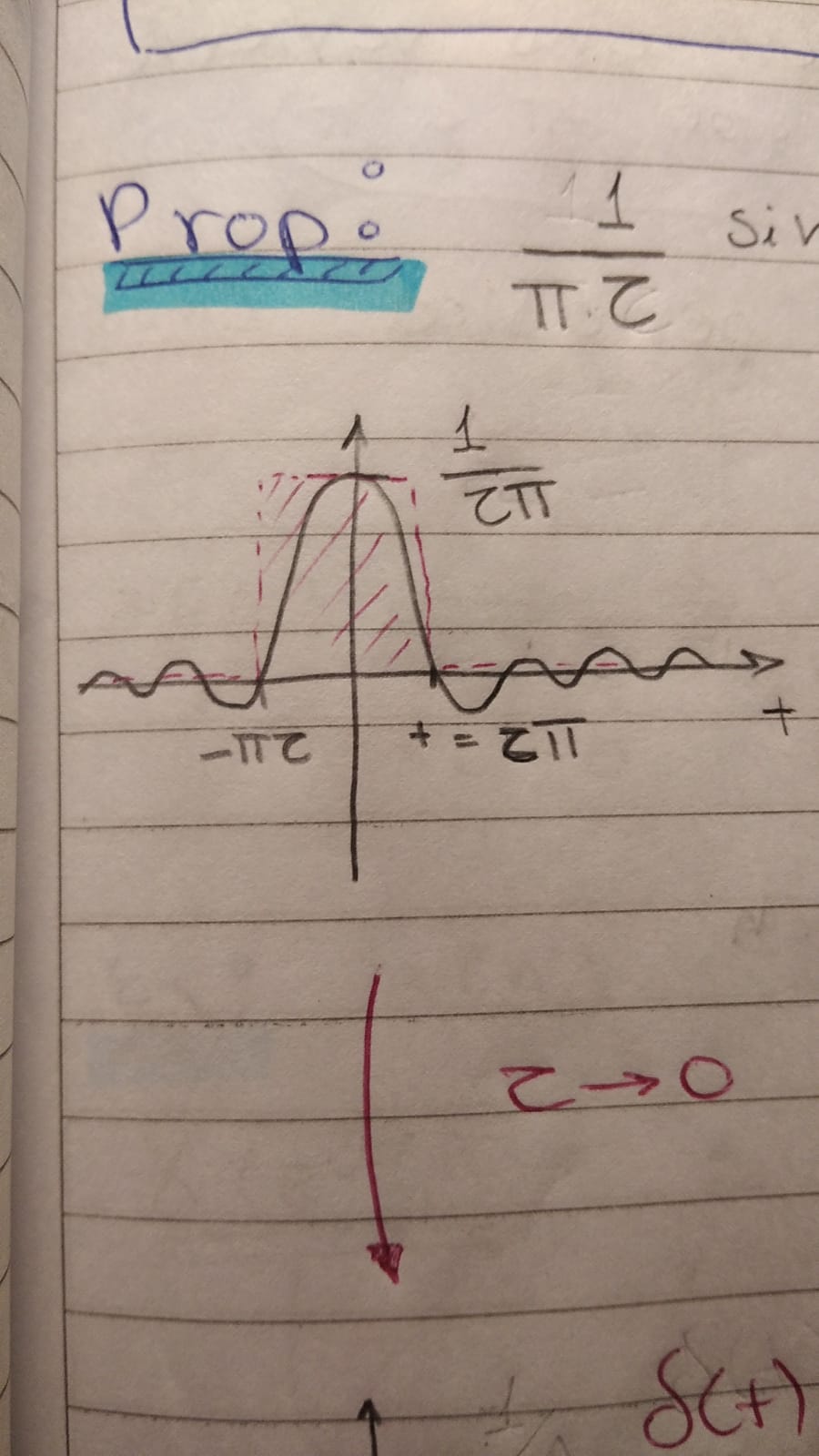
Lo que decís es correcto. El pulso rojo no es una muy buena aproximación para ver la delta, ya que su área no coincide con el área del sinc (que es 1).
Si bien te deja ver que el ancho se achica mientras la altura aumenta, no lo hace con área 1.
Si bien te deja ver que el ancho se achica mientras la altura aumenta, no lo hace con área 1.
El pulso correcto para eso sería uno con la mitad de altura.