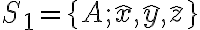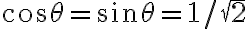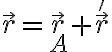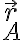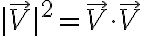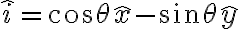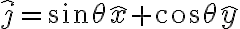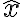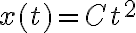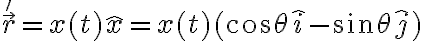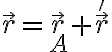Hola tengo algún problema con este en la parte a), mi planteo es este:
La energía cinética es T=(1/2)mv^2, así que hay que hallar v. Dentro de la nave no se percibe vo, pues si alguien está dentro de la nave no notará la velocidad en la que asciende me parece. Esta parte me dio bien, planteado así:
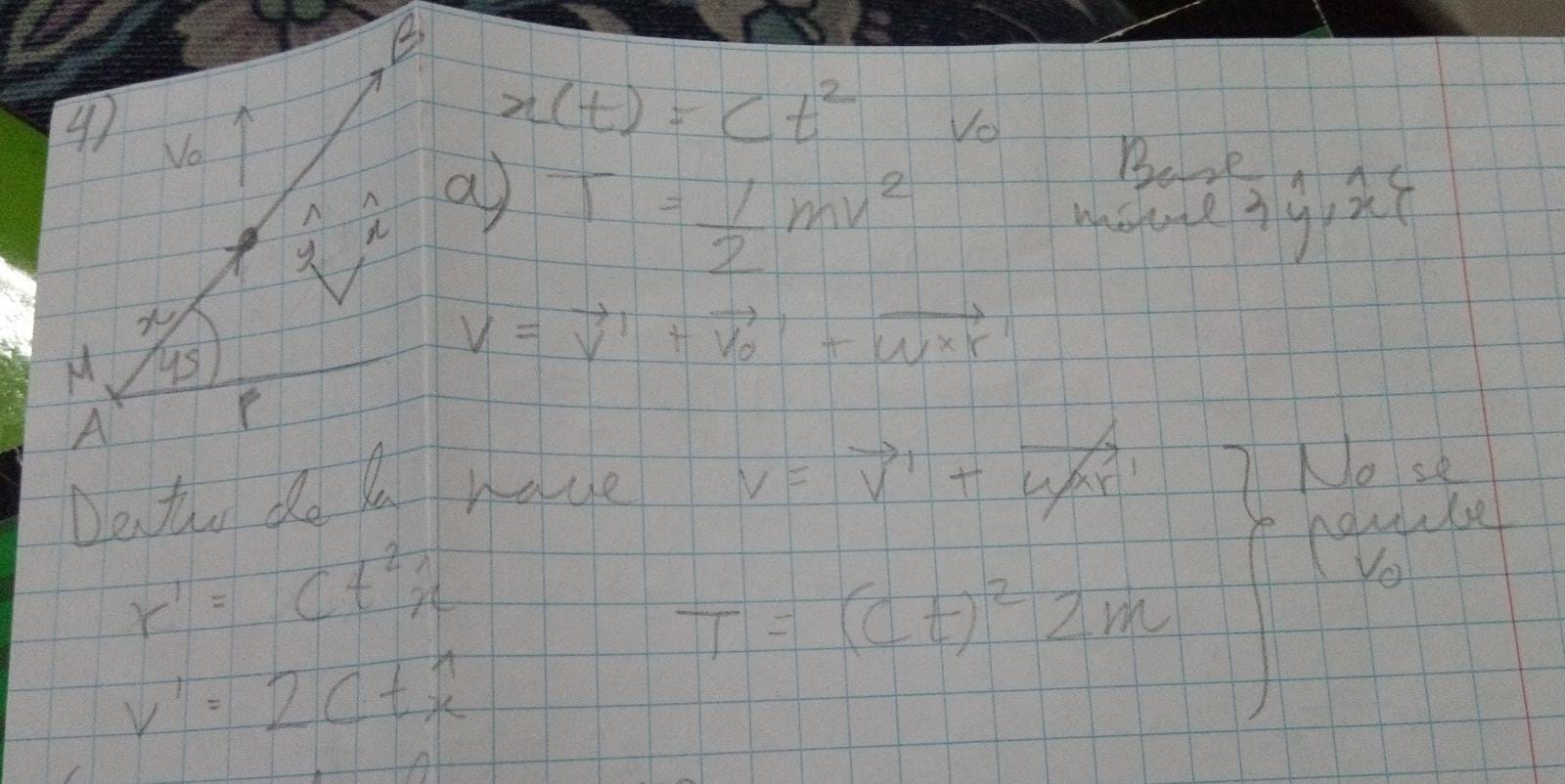
el tema es que no me da la siguiente parte, que para mí es básicamente lo mismo pero ahora sí se percibe vo'. Lo planteé así:
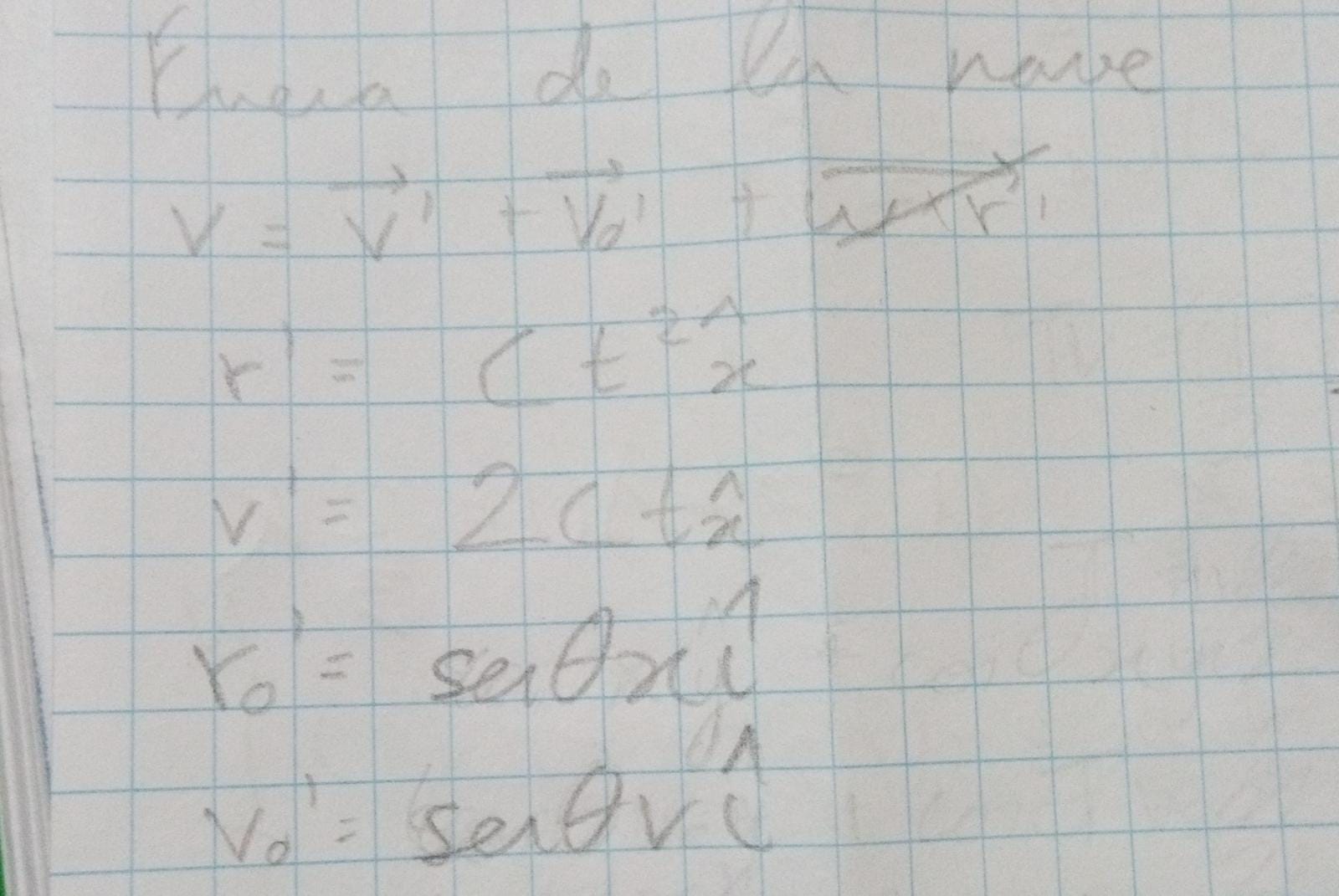
me dio con sen porque según me parece, la base móvil está en el punto A que en la primer foto está abajo a la izquierda, mientras que mi base fija tiene centro en la F que está al lado de la A en la misma foto, está con otros versores porque mi idea era representar la distancia ro' con versores de la base fija y traducirlos a la base móvil para que se haga más fácil pero creo que me estoy liando un poco, este dibujo representa más o menos mi idea:
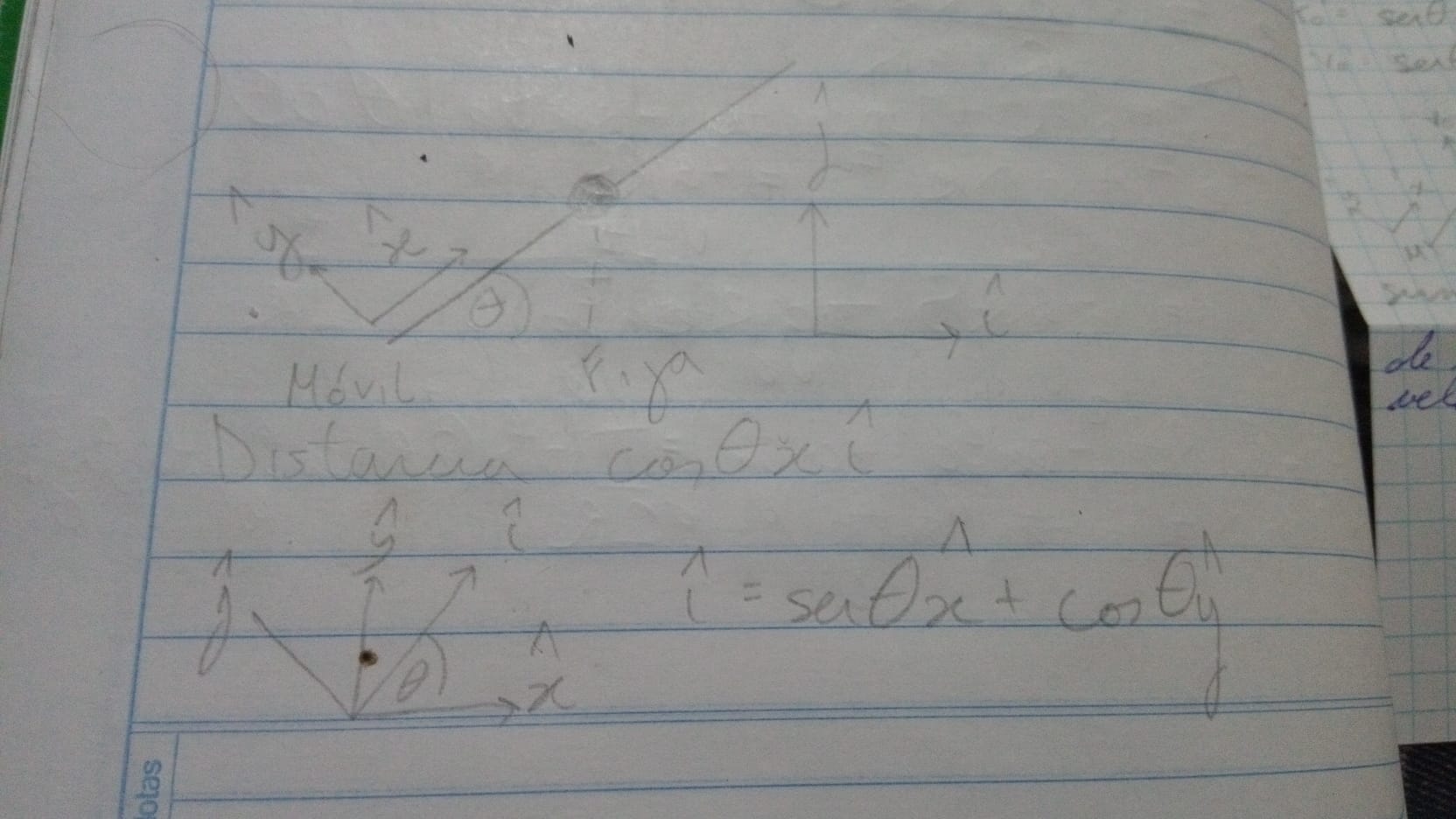
me queda un poco deforme pero mi idea era esa
graciass
(Editado por Nicolás Casaballe: reajuste del tamaño de las imágenes - envío original jueves, 31 de marzo de 2022, 21:01)