hola:
creo que en vez de pensarlo por paridad, lo más fácil es directamente modelar el juego con las reglas dadas:
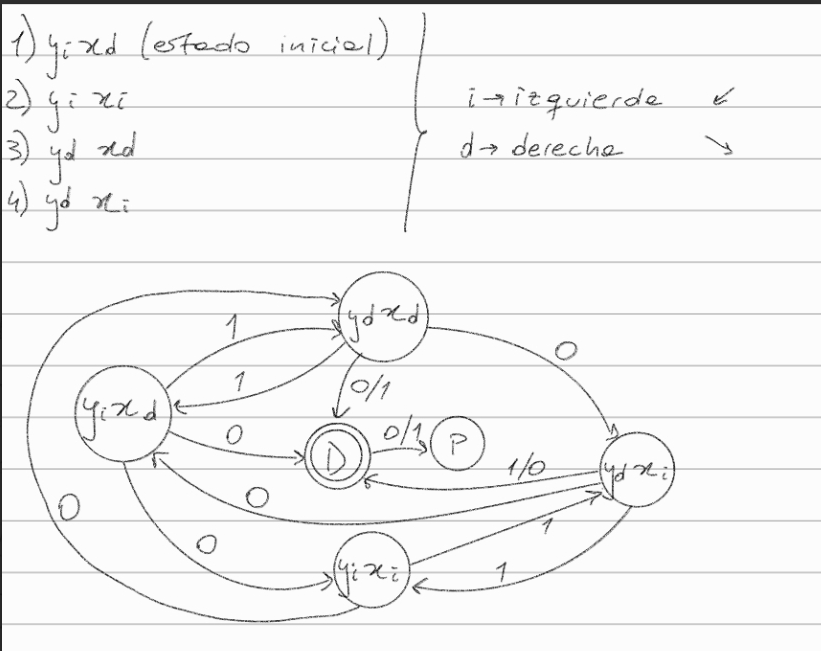
el estado del juego está dado por la configuración de las llaves. así, (x: <, y:<), (x:<, y:>), (x:<, y:<) serían algunos estados del autómata. por ejemplo, el estado del dibujo sería (>,<). si yo pongo en ese estado una ficha por A (leo un 1), el siguiente estado sería (>,>), ya que solo cambia el valor de y.
luego, ¿qué sucede con la aceptación de la tira? para eso hay que considerar que si sale por D, el estado resultante debería ser final... con lo que se pueden duplicar tus estados. por ejemplo, podrías tener un estado (<,<) y otro ((<,<)) para indicar que en un caso la última ficha salió por C y en el otro por D, dejando el juego en la configuración x:< e y:<.
saludos,
d.-
creo que no es necesario usar un AFND, dado que, puesta una ficha por A o B, la configuración resultante está determinada.