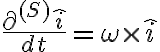Buenas, tengo una duda con respecto a las derivadas e sub theta y e sub Phi. No me queda claro como llega a eso. Gracias
En respuesta a Martina Montichelli Aplanalp
Re: Duda resolución ejercicio 9
de Valentina Chagas Bas -
Hola, me parece que la manera más fácil de derivar un versor de un sistema móvil en el tiempo es utilizar el resultado:
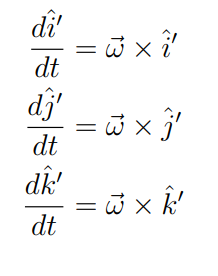
donde w es la velocidad angular total del sistema (notas de mecánica newtoniana pag 14).
No se bien como están puestos tus versores pero por el resultado supongo que la base {eϕ, eρ,k} es la que gira solo según phi y la otra base {eθ, ex,k} es la que gira según phi y theta.
Bueno para derivar eϕ:
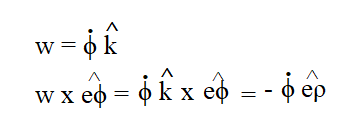
donde el w usado es el de la base {eϕ, eρ,k} y el producto de los versores con la regla de la mano derecha.
Para el otro versor es lo mismo nada mas que esta base además de girar con un ángulo phi también gira según theta y con la regla de la mano derecha te queda según ex.
Ahora, si este método no te convence el método largo es ver de que ángulos depende el versor y plantear las derivadas parciales como esta en openfing.
Igual espera a que te conteste un profe porque podría estar mal.
Saludos!
180 palabras
Hola,
La respuesta de Valentina está esencialmente bien. La idea clave es la siguiente: supongamos que yo quiero hallar la derivada de los versores de una base, del punto de vista de un sistema de referencia . Es decir quiero calcular algo del estilo
. Es decir quiero calcular algo del estilo
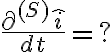
donde crucialmente la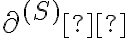 denota que la derivada se est\'a haciendo del punto de vista del sistema
denota que la derivada se est\'a haciendo del punto de vista del sistema  . Entonces la forma de hacerlo es encontrar un sistema de referencia
. Entonces la forma de hacerlo es encontrar un sistema de referencia 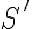 en el cual los versores est'an en reposo (ej, en la notaci'on que estoy usando esto quiere decir
en el cual los versores est'an en reposo (ej, en la notaci'on que estoy usando esto quiere decir 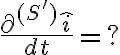 ). Sea
). Sea 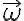 la velocidad angular de
la velocidad angular de 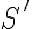 respecto a
respecto a  . Entonces se cumple que
. Entonces se cumple que
La respuesta de Valentina está esencialmente bien. La idea clave es la siguiente: supongamos que yo quiero hallar la derivada de los versores de una base, del punto de vista de un sistema de referencia
 . Es decir quiero calcular algo del estilo
. Es decir quiero calcular algo del estilo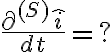
donde crucialmente la
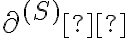 denota que la derivada se est\'a haciendo del punto de vista del sistema
denota que la derivada se est\'a haciendo del punto de vista del sistema  . Entonces la forma de hacerlo es encontrar un sistema de referencia
. Entonces la forma de hacerlo es encontrar un sistema de referencia 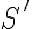 en el cual los versores est'an en reposo (ej, en la notaci'on que estoy usando esto quiere decir
en el cual los versores est'an en reposo (ej, en la notaci'on que estoy usando esto quiere decir 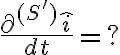 ). Sea
). Sea 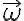 la velocidad angular de
la velocidad angular de 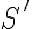 respecto a
respecto a  . Entonces se cumple que
. Entonces se cumple que Para aplicarlo en este ejercicio hay que hacer básicamente lo que dijo valentina. Para derivar 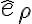 y
y 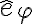 respecto al tiempo del punto de vista del sistema fijo, usando la f'ormula, hay que ver con que velocidad angular se mueve esta base de versores (o lo que es lo mismo, con que velocidad angular se mueve un sistema de referencia que los ve inm'oviles) respecto al sistema fijo. Esa velocidad angular es simplemente
respecto al tiempo del punto de vista del sistema fijo, usando la f'ormula, hay que ver con que velocidad angular se mueve esta base de versores (o lo que es lo mismo, con que velocidad angular se mueve un sistema de referencia que los ve inm'oviles) respecto al sistema fijo. Esa velocidad angular es simplemente 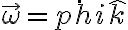 .
.
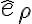 y
y 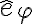 respecto al tiempo del punto de vista del sistema fijo, usando la f'ormula, hay que ver con que velocidad angular se mueve esta base de versores (o lo que es lo mismo, con que velocidad angular se mueve un sistema de referencia que los ve inm'oviles) respecto al sistema fijo. Esa velocidad angular es simplemente
respecto al tiempo del punto de vista del sistema fijo, usando la f'ormula, hay que ver con que velocidad angular se mueve esta base de versores (o lo que es lo mismo, con que velocidad angular se mueve un sistema de referencia que los ve inm'oviles) respecto al sistema fijo. Esa velocidad angular es simplemente 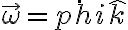 .
.Cuando vamos a derivar 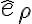 y
y 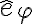 respecto al sistema fijo es la misma idea, teniendo cuidado que la velocidad con la que rotan estos versores respecto al sistema fijo es distinta que en el caso anterior. en este caso tenemos
respecto al sistema fijo es la misma idea, teniendo cuidado que la velocidad con la que rotan estos versores respecto al sistema fijo es distinta que en el caso anterior. en este caso tenemos 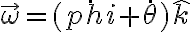 .
.
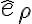 y
y 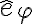 respecto al sistema fijo es la misma idea, teniendo cuidado que la velocidad con la que rotan estos versores respecto al sistema fijo es distinta que en el caso anterior. en este caso tenemos
respecto al sistema fijo es la misma idea, teniendo cuidado que la velocidad con la que rotan estos versores respecto al sistema fijo es distinta que en el caso anterior. en este caso tenemos 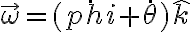 .
.Si no te resulta evidente por qu'e son estas las velocidades angulares, no dudes en preguntarlo y vemos la explicación más en detalle.
Por cierto, otra forma de hacer esto es proyectar todos los versores en una base de versores fija del punto de vista del sistema fijo. Ahí hacer las derivadas es bastante fácil: sólo es necesario derivar las componentes.
En fin, espero que esto les sirva, de lo contrario no duden en volver a preguntar.
saludos
Guzmán
316 palabras
Hola. Mi pregunta es si los ángulo varian uniformemente con el tiempo o debo pensar que es cualquier función del tiempo. pregunto porque en esos caso la derivada es cero
30 palabras
En respuesta a Elena Lourdes García García
Re: Duda resolución ejercicio 9
Hola!
Siempre que en la letra no se explicite lo contrario, los ángulos serán una función arbitraria del tiempo.
Saludos!
Siempre que en la letra no se explicite lo contrario, los ángulos serán una función arbitraria del tiempo.
Saludos!
20 palabras