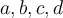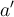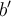Buenas, queria consultar sobre una parte de una ejercicio de las notas de teorico,

En especial la ultima parte donde dice: "Si consideramos.... y haciendo cuentas llegamos a que ...."
Lo que no me queda claro es la parte que dice, "haciendo cuentas llegamos a que", intente realizar las cuentas correspondiente pero no llegue a nada certero, ni al mismo resultado, iguale las condiciones a la ecuacion por definicion de Moebius, teniendo encuenta de que z= -d/c por la tercer ecuacion que da infinito, pero no llegue a nada, espero que me puedan guiar mas o menos por si me perdi algo.

Espero que se entienda la letra.
Posdata: Pregunto en el foro del curso porque en el foro de teorico se ve que no lleguan las notificaciones o algo
Saludos cordiales
Diego