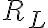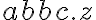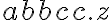[Ejercicio 4] [Parte b] [Parte 2]

[Ejercicio 4] [Parte b] [Parte 2]

de Bruno Stefano Lombardo Palleiro -
Número de respuestas: 3

Buenas, en este caso la tira x=abbc es un prefijo de la tira y=abbcc, entonces ambas tienen el mismo n y k.  Por lo tanto, las restricciones respecto a la cantidad de "a" y de "b" que van luego de las j  "c" , son las mismas en ambas tiras

A su vez, como no hay restricciones de tope para j , la cantidad de "c" que haya al principio de cualquier tira z no influirá .

Entonces para cada tira z , hay que analizar a partir de la primera ocurrencia que no sea una "c".  Si aquí se cumple que hay  2 "a" y luego una "b",  tanto xz como yz estarán en Lb y en cualquier otra situación no.

 Por lo que la afirmación es verdadera 

Es correcta esta idea? Y en caso de serla, es necesario formalizarla mas, o con esto alcanza?

saludos

En respuesta a Bruno Stefano Lombardo Palleiro

Re: duda ej 4 parte 2

de Santiago Gongora -
Vas re bien. Pero como te imaginarás no te voy a decir la respuesta :P

Para estar seguro de lo que estás diciendo, intentá construir un lenguaje por comprensión de todo lo que podés concatenarle a ambas tiras para que sigan perteneciendo al lenguaje. Eso ya lo hiciste escribiéndolo en el mensaje, pero formalizalo en un conjunto por comprensión.
Lo que vas a obtener acá es el lenguaje de las tiras z (de la definición de R_L ) que al concatenarlas, las tiras resultantes (abbc.z y abbcc.z) pertencen (ambas) al lenguaje.

¿Y qué pasa si las tiras z no pertenecen al lenguaje ese que te definiste por comprensión? ¿Puede pasar que algunas, al concatenarlas, hagan que la tira de la izquierda esté en el lenguaje y la de la derecha no (o vice versa)?

Con que reflexiones sobre esto y lo escribas, ya para el ejercicio es suficiente. En este ejercicio no buscamos tanta formalización, sino que queremos que se empapen del funcionamiento de la relación R_L . Luego veremos métodos formales para hacer este tipo de chequeos.

Cualquier cosa me decís.

Saludos,
Santi
En respuesta a Santiago Gongora

Re: duda ej 4 parte 2

de Bruno Stefano Lombardo Palleiro -
Hola Santi, gracias por la respuesta!
Te escribo lo que pensé a partir de lo que me dijiste, para saber si el ejercicio está terminado.

El conjunto que me indicaste sería L={c^p . a^2 . b :p>=0 }
Entonces si z e L , ya vimos por lo que dije en el primer mensaje que abbcz e L y abbcc e L.

SI z no pertenece a L, puede pasar que abbcz e Lb?
Si suponemos que si, z puede empezar de la forma z=c^k.w con k>=0 peor luego w=a^2.b ya que sino no se cumpliría que abbcz e Lb , entonces tenemos que z e L y es absurdo
Por lo tanto para todo z que no pertenece a L, abbcz no pertenece a Lb.

De manera muy similar se puede mostrar que para todo z que no pertenece a L, abbccz no pertenece a Lb.

Entonces no puede pasar que si z no pertenece a L cumpla esos casos que me dijiste y como consideramos todo z perteneciente sigma asterisco , la afirmación es verdadera.