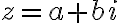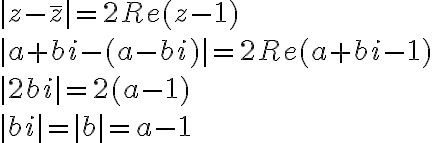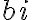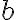Buenas, en este ejercicio luego de hacer cuentas llego a que a-b=1. Me fije en las respuestas y me queda algo diferente. Yo lo interpreto como una recta que pasa por el (1,0) y el (0,-1) solamente. Adjunto la imagen de la respuesta para ver si me pueden explicar de donde sale la parte que circulé con azul y por qué por ejemplo el punto (0,-1) no esta en la respuesta que es lo que no entiendo.
Gracias.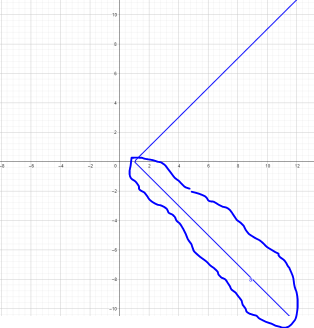
Me pasó lo mismo, en mi caso interpreté el || como modulo no como valor absoluto, entonces me quedó
|2bi| = 2(a-1)
|2bi| = 2(a-1)
2b=2(a-1)
b=2(a-1)
Y termino con la grafica sin el valor absoluto
Es lo mismo interpretarlo como módulo o como valor absoluto. El valor absoluto es el módulo pero restricto sólo a los reales (el módulo de 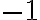 es
es  ). De un lado tenés el módulo de
). De un lado tenés el módulo de 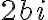 y sacás el
y sacás el 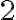 para afuera y eso, pero cuando decís que el módulo de
para afuera y eso, pero cuando decís que el módulo de  es
es  , estás cometiendo un error, porque si
, estás cometiendo un error, porque si  es negativo, no tiene sentido que el módulo sea una cosa negativa.
es negativo, no tiene sentido que el módulo sea una cosa negativa.
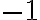 es
es  ). De un lado tenés el módulo de
). De un lado tenés el módulo de 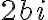 y sacás el
y sacás el 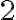 para afuera y eso, pero cuando decís que el módulo de
para afuera y eso, pero cuando decís que el módulo de  es
es  , estás cometiendo un error, porque si
, estás cometiendo un error, porque si  es negativo, no tiene sentido que el módulo sea una cosa negativa.
es negativo, no tiene sentido que el módulo sea una cosa negativa.