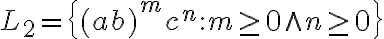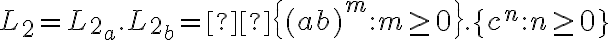TeoLeng: [Ejercicio 3] Duda con la inducción

Buenas noches,

En este ejercicio se solicita el uso de inducción en la prueba, pero no entiendo el uso de esta heramienta en este caso en particular (idem para la parte b).

La duda surge del hecho que se puede probar la tesis inductiva sin utilizar la hipótesis inductiva, por lo tanto, la prueba de la tesis inductiva es en realidad la prueba completa.

Por ejemplo en la parte a)

Si hacemos inducción sobre k, el paso inducido nos quedaría asi:

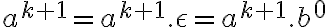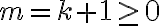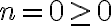$a^{k+1} = a^{k+1}.\epsilon = a^{k+1}.b^0$ y como $m = k + 1 \geq 0$ y $n = 0 \geq 0$ . Por definición conjunto de la derecha, 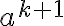$a^{k+1}$ pertenece. Pero en esta prueba en ningún punto se utiliza la hipótesis inductiva ( 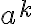$a^{k}$ pertenece).

( Creo que puedo utilizar que 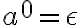$a^0 = \epsilon$ , ya que para cualquier alfabeto 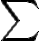$\sum{}$ y para cualquier 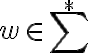$w \in \sum^{*}$ , se cumple que 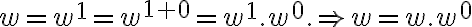$w = w^1 = w^{1+0} = w^1 . w^0. \Rightarrow w = w . w^0$ . Y como estamos hablando de "concatenación" de strings, se debe cumplir que 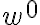$w^0$ es la cadena vacía- ¿Este razonamiento es correcto?)

Por lo tanto, ¿cómo estaría correctamente usada la inducción en este ejercicio?

Saludos y gracias

Daniel.

Re: Duda con la inducción del ejercicio 3

de Santiago Gongora - lunes, 7 de marzo de 2022, 10:00

¡Hola Daniel!

Lo que queremos con este ejercicio es que:

Practiquen la elección del índice de inducción, que lo hiciste bien.
Practiquen el planteamiento de Paso Base y Paso Inductivo, que no lo pusiste en el mensaje pero entiendo que sí lo planteaste. Al plantear estos pasos, lo que estamos probando es que todas las tiras que surgen de variar el índice k van a pertenecer al lenguaje de la derecha y, por lo tanto, que el lenguaje de la izquierda está incluido en el de la derecha.
Experimenten con la visualización de los lenguajes como conjuntos. Por ejemplo, al lenguaje $L_2 = \{(ab)^m c^n: m \geq 0 \wedge n \geq 0\}$ lo podemos ver como la concatenación de otros dos lenguajes: $L_2 = L_{2_a}.L_{2_b} = \{(ab)^m: m \geq 0\}.\{c^n: n \geq 0\}$
Hagan el razonamiento de las potencias y la tira vacía que, correctamente, mostraste en tu mensaje.

En posteriores prácticos haremos pruebas por inducción (bastante) más complicadas, por lo que objetivo del ejercicio no es entreverarse con las cuentas sino repasar los conceptos. Por eso puede que el "remate" de la prueba te desconcierte al ser extremadamente sencillo.

Cualquier duda a las órdenes.

Saludos,
Santi