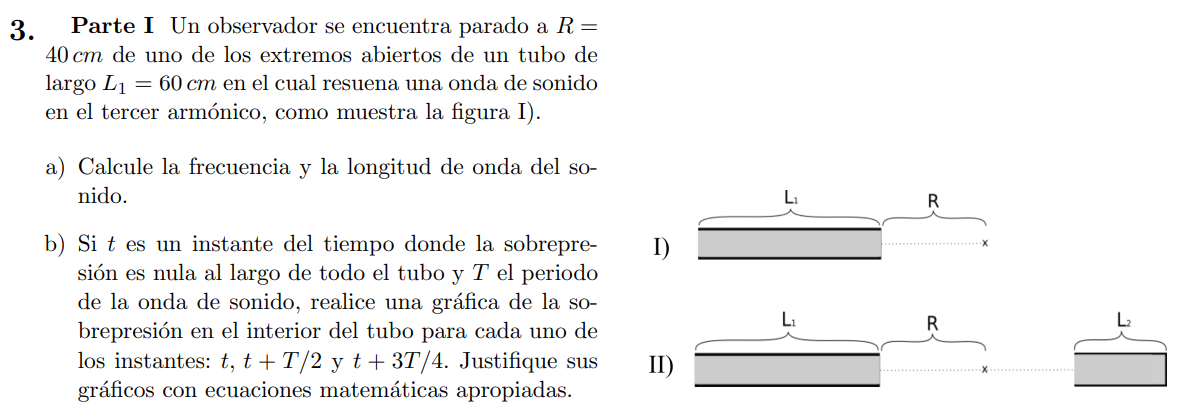
Buenas tardes,
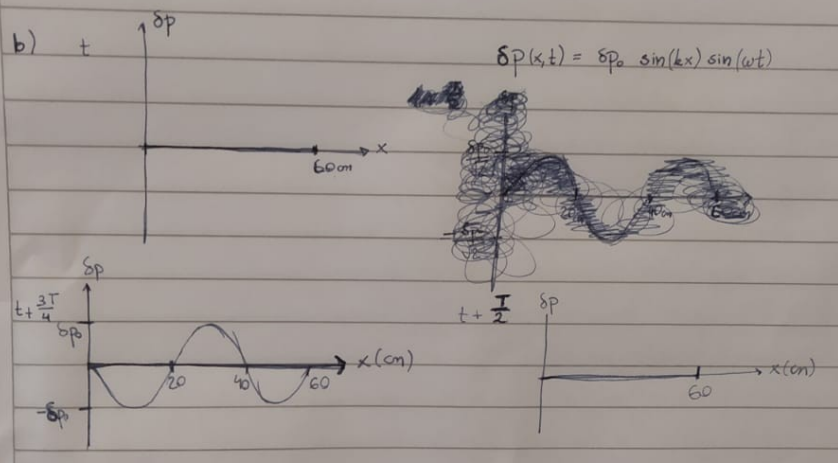
En este caso, las condiciones de borde te dicen que debe haber dos nodos de sobrepresión en los bordes. Esto lleva a patrones de onda estacionarias equivalentes a los de la cuerda fijada a dos paredes. Matemáticamente esos patrones sabemos que se escriben como superposición de dos ondas viajeras que se mueven en sentidos opuestos. Esto te lleva a la ecuación que está en la esquina superior derecha de la imagen. Fijate que hay una dependencia temporal que lo que hace es modular el patrón y hay t para los que sin(wt) = 0 y que w = 2*Pi / T. A partir de ello puedes encontrar los patrones.
Espero que esto aclare tu duda. Avisanos cualquier cosa.
Saludos,
Carlos