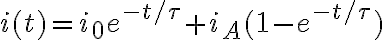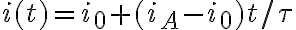Hola,
Respecto a tu primera consulta el ejercicio se puede hacer bien con cualquier sistema de coordenadas mientras uno trabaje de manera coherente. En tus coordenadas la integral queda
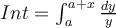
Bajo el cambio de variable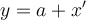 esto es equivalente a lo que plantea la solución.
esto es equivalente a lo que plantea la solución.
Con respecto a tu segunda pregunta, I2 e I3 tienen el mismo módulo y defasajes opuestos respecto a V. Es por esto que la suma de estos complejos (o suma vectorial en el plano) te da algo que es colineal con V. Las tres corrientes sin embargo no son iguales.
Respecto a tu primera consulta el ejercicio se puede hacer bien con cualquier sistema de coordenadas mientras uno trabaje de manera coherente. En tus coordenadas la integral queda
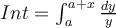
Bajo el cambio de variable
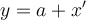 esto es equivalente a lo que plantea la solución.
esto es equivalente a lo que plantea la solución.Con respecto a tu segunda pregunta, I2 e I3 tienen el mismo módulo y defasajes opuestos respecto a V. Es por esto que la suma de estos complejos (o suma vectorial en el plano) te da algo que es colineal con V. Las tres corrientes sin embargo no son iguales.
Con respecto a tu tercera pregunta, 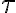 es simplemente un parámetro del problema que te da el tiempo característico del decaimiento exponencial hacia el valor asintótico (por eso aparece justamente en el exponente de la parte exponencial de la solución para la corriente). Este tiempo se puede hallar en términos de los parámetros el circuito resolviendo la ecuación diferencial. Para ver como sacarlo de la gráfica, observa que la solución para la corriente se puede escribir de esta forma:
es simplemente un parámetro del problema que te da el tiempo característico del decaimiento exponencial hacia el valor asintótico (por eso aparece justamente en el exponente de la parte exponencial de la solución para la corriente). Este tiempo se puede hallar en términos de los parámetros el circuito resolviendo la ecuación diferencial. Para ver como sacarlo de la gráfica, observa que la solución para la corriente se puede escribir de esta forma:
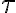 es simplemente un parámetro del problema que te da el tiempo característico del decaimiento exponencial hacia el valor asintótico (por eso aparece justamente en el exponente de la parte exponencial de la solución para la corriente). Este tiempo se puede hallar en términos de los parámetros el circuito resolviendo la ecuación diferencial. Para ver como sacarlo de la gráfica, observa que la solución para la corriente se puede escribir de esta forma:
es simplemente un parámetro del problema que te da el tiempo característico del decaimiento exponencial hacia el valor asintótico (por eso aparece justamente en el exponente de la parte exponencial de la solución para la corriente). Este tiempo se puede hallar en términos de los parámetros el circuito resolviendo la ecuación diferencial. Para ver como sacarlo de la gráfica, observa que la solución para la corriente se puede escribir de esta forma:donde en esta expresión 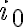 es el valor inicial de la corriente e
es el valor inicial de la corriente e 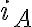 es el valor asintótico. Para tiempos cortos esto se comporta como una recta
es el valor asintótico. Para tiempos cortos esto se comporta como una recta
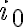 es el valor inicial de la corriente e
es el valor inicial de la corriente e 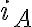 es el valor asintótico. Para tiempos cortos esto se comporta como una recta
es el valor asintótico. Para tiempos cortos esto se comporta como una rectaY esta recta es justamente la que se grafica en la letra del ejercicio. En la letra te dicen que esta recta toma el valor de la asíntota en un tiempo dado. De la ecuación anterior es claro que ese tiempo es 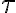 . Como de la ec dif se halla
. Como de la ec dif se halla 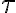 en t
en t
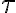 . Como de la ec dif se halla
. Como de la ec dif se halla 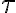 en t
en ttérminos de los parémetros del problema, de ahí se obtiene la solución.
espero que esto responda tus preguntas
de lo contrario no dudes en repreguntar
saludos
g