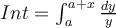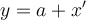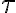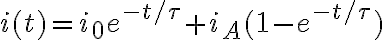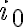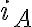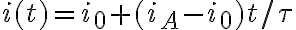F3 - 2S: dudas examenes 2016 y 2018 dic

Hola, tengo un par de dudas sobre estos parciales.

En el de 2016, ejercicio 2 parte a, no entiendo como darme cuenta qué extremos tomar. Yo habia tomado el 0 de referencia en el cable, entonces puse como extremos de la integral del flujo : a y (a + x), y en la solucion toman el 0 donde arranca el circuito. Como se cual usar? porque me hubiese quedado distinto.

Y la otra duda es sobre la parte d de ese mismo ejercicio, hallé los angulos de desfasaje de i2 y i3 y me dan iguales y opuestos, y supongo que como i1 es la suma vectorial de estas dos, es por eso que i1 queda sobre el mismo eje que V, esto es asi? Porque me cuesta entender cómo pueden valer lo mismo las 3 intensidades si hay un nodo.

Con respecto al parcial 2018, me podrian explicar la solucion de la parte 2c?. No entiendo que significa ese τ (constante de tiempo) , y cómo deberia yo identificarla en la grafica.

Gracias, saludos

Re: dudas examenes 2016 y 2018 dic

de Guzman Hernandez - lunes, 20 de diciembre de 2021, 15:55

Hola,

Respecto a tu primera consulta el ejercicio se puede hacer bien con cualquier sistema de coordenadas mientras uno trabaje de manera coherente. En tus coordenadas la integral queda

Bajo el cambio de variable

esto es equivalente a lo que plantea la solución.

Con respecto a tu segunda pregunta, I2 e I3 tienen el mismo módulo y defasajes opuestos respecto a V. Es por esto que la suma de estos complejos (o suma vectorial en el plano) te da algo que es colineal con V. Las tres corrientes sin embargo no son iguales.

Con respecto a tu tercera pregunta,

$\tau$ es simplemente un parámetro del problema que te da el tiempo característico del decaimiento exponencial hacia el valor asintótico (por eso aparece justamente en el exponente de la parte exponencial de la solución para la corriente). Este tiempo se puede hallar en términos de los parámetros el circuito resolviendo la ecuación diferencial. Para ver como sacarlo de la gráfica, observa que la solución para la corriente se puede escribir de esta forma:

$i(t) = i_0 e^{-t/\tau} + i_A(1-e^{-t/\tau})$

donde en esta expresión

$i_0$ es el valor inicial de la corriente e

$i_A$ es el valor asintótico. Para tiempos cortos esto se comporta como una recta

$i(t) = i_0 + (i_A-i_0)t/\tau$

Y esta recta es justamente la que se grafica en la letra del ejercicio. En la letra te dicen que esta recta toma el valor de la asíntota en un tiempo dado. De la ecuación anterior es claro que ese tiempo es

$\tau$ . Como de la ec dif se halla

$\tau$ en t

términos de los parémetros del problema, de ahí se obtiene la solución.

espero que esto responda tus preguntas

de lo contrario no dudes en repreguntar

saludos