
Hola, en este ejercicio cuando calculo el limite de g por polares me da 0, pero en la solucion dice que no existe, no entiendo que es lo que esta mal y si quiza no se puede calcular por polares, gracias

Hola, en este ejercicio cuando calculo el limite de g por polares me da 0, pero en la solucion dice que no existe, no entiendo que es lo que esta mal y si quiza no se puede calcular por polares, gracias
Hola. Al pasar el límite a polares queda 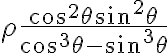 . Acordate que para asegurar que el límite da 0 con polares precisás poder escribir al límite como algo de la forma
. Acordate que para asegurar que el límite da 0 con polares precisás poder escribir al límite como algo de la forma 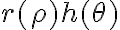 , con
, con 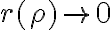 cuando
cuando 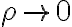 y
y 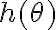 una función acotada. En este caso
una función acotada. En este caso 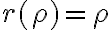 , que tiende a 0 con
, que tiende a 0 con 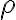 , pero
, pero 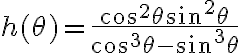 no es una función acotada (en particular, en los puntos donde
no es una función acotada (en particular, en los puntos donde 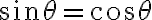 se va a infinito). Por eso no sirve usar polares en este caso.
se va a infinito). Por eso no sirve usar polares en este caso.
Saludos
Hola. Para la pregunta 1, en general lo que pasa es que primero probás hacer el límite por rectas (o polares, que en el fondo es mirar por rectas). Si el límite da distinto entre distintas rectas entonces podés afirmar que el límite no existe, pero si da lo mismo por cualquier recta eso no te alcanza para probar que el límite existe. Ahí es cuando probás con alguna otra curva.
Para la segunda pregunta no hay una respuesta general. Qué curva probar depende de la función que estés considerando, y en general cómo elegirla depende de la experiencia previa. En ese sentido, es similar a cuando estás buscando la primitiva de alguna función: ahí no hay una regla explícita sobre qué método (partes, cambio de variable, etc) probar, la experiencia con otros ejercicios y la "pinta" de la función te dan intuición sobre qué método probar. En este caso, la idea es que la función 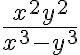 se va a infinito sobre la recta
se va a infinito sobre la recta 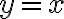 . Si te fijás, la curva
. Si te fijás, la curva 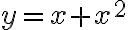 en
en  es tangente a la recta
es tangente a la recta 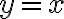 : la idea de considerar esa curva es justamente acercarte a
: la idea de considerar esa curva es justamente acercarte a  de una forma que sea parecida a
de una forma que sea parecida a 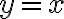 .
.
En esta pregunta "¿tendría que hacer 4 límites y si uno es distinto el límite de la función ya no existe?" no entendí a qué cuatro límites te referís. Límites direccionales se puede usar para cualquier función.
Saludos