- Una cláusula es una multiplicación de variables booleanas igualada a cero, donde el cero representa true. Ejemplo:
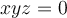 si
si 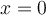 o
o 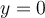 o
o 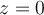 , con
, con 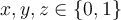
- El problema de satisfacibilidad no es más que un sistema de ecuaciones donde cada ecuación es un producto de variables booleanas igualado a cero.
- Para resolver este sistema de ecuaciones debemos de separar en casos, si cierta variable vale cero o si no.
- Separar en casos es en otras palabras probar valores para las variables.
- Por lo tanto el problema de satisfacibilidad no puede resolverse de otra forma que no sea probando valores hasta llegar a la solución.
- Conclusión: el problema de satisfacibilidad no pertenece a P.
Nota: cuando separamos en casos no podríamos descartar ninguno de antemano porque para una situación del problema genérica todos los casos tienen "igual probabilidad" de aportar una solución.
No sé si realmente sea válido el razonamiento pero quería compartirlo por si llega a aportar algo jaja. Estaría bueno si pudieran hacerle alguna crítica o corrección, de todas formas no les quiero quitar mucho tiempo. Saludos