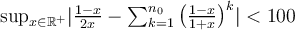Novedades

Hola,

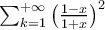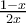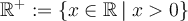hoy en clase demostramos que la serie $\sum_{k=1}^{+\infty} \left(\frac{1-x}{1+x}\right)^2$ converge puntualmente a $\frac{1-x}{2x}$ en $\mathbb{R}^+ := \{x \in \mathbb{R} \left|\right. x>0\}$. También probamos que la serie no converge uniformemente en 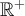$\mathbb{R}^+$. Para ver esto lo que hicimos fue usar el criterio de Cauchy.

Otra forma de ver esto último es ir por absurdo. Supongamos que la serie converge uniformemente en 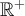$\mathbb{R}^+$, entonces existe 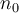$n_0$ tal que

$\sup_{x \in \mathbb{R}^+} \lvert \frac{1-x}{2x} - \sum_{k=1}^{n_0}\left(\frac{1-x}{1+x}\right)^k\rvert < 100$

sin embargo esto es absurdo ya que 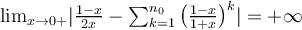$\lim_{x\to 0+} \lvert \frac{1-x}{2x} - \sum_{k=1}^{n_0}\left(\frac{1-x}{1+x}\right)^k\rvert = +\infty$.

También dijimos que la serie convergía uniformemente en cualquier compacto incluido en 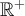$\mathbb{R}^+$. Esto lo pueden probar usando la mayorante de Weierstrass, les dejo intentarlo!!

Saludos!