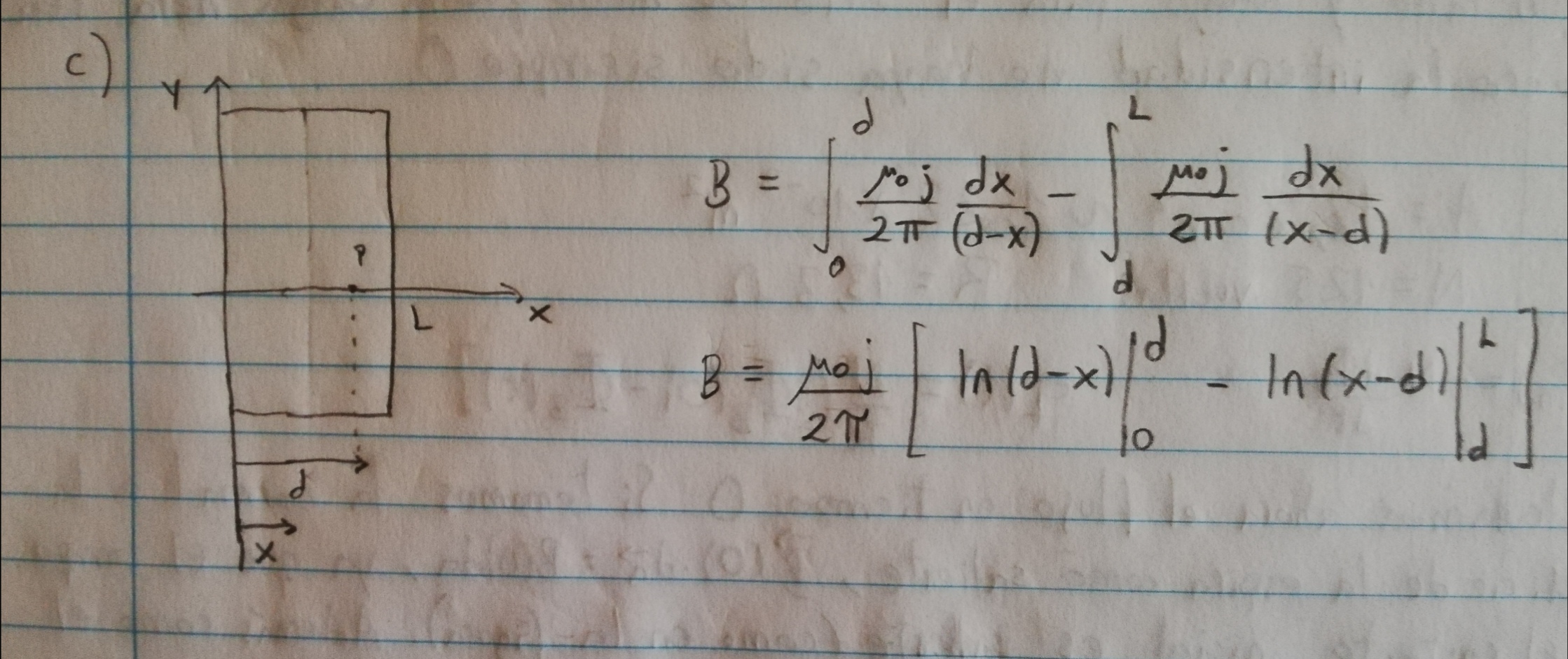Buenas
Mi duda es respecto a la densidad de corriente, no comprendo muy bien como la define en este ejercicio, ya que yo definiría a j como i/A pero en las solución la define como una densidad lineal di/dx. Además en la letra dice que la densidad de corriente se define en el sentido positivo de la coordenada y. ¿En el caso de las soluciones no la estaría definiendo en el sentido de la coordenada x?
Gracias de antemano por la ayuda, saludos!