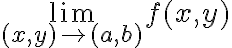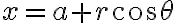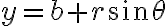Coordenadas polares - Límites y continuidad en R^n

Coordenadas polares - Límites y continuidad en R^n

de Thiago Caetano Acuña Vinoles -
Número de respuestas: 4

Buenas tardes, tengo una duda teórica:

Cuando se introduce el concepto de coordenadas polares y el escribir a los puntos del plano en dicha notación para calcular límites, siempre son límites en 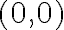(0,0)  , ¿no? 
Es decir, límites de la forma: 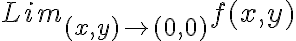 Lim_{(x,y) \rightarrow(0,0)} f(x,y)

Esto, entiendo yo, es porque las coordenadas polares están definidas a partir del punto 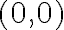 (0,0) (módulo+ángulo).

¿Hay alguna forma de poder usar esta herramienta para límites que no sean en 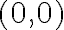 (0,0) ?


Saludos, 
En respuesta a Thiago Caetano Acuña Vinoles

Re: Coordenadas polares - Límites y continuidad en R^n

de Bernardo Marenco -

Hola Thiago. Algo que podés hacer es escribir las coordenadas polares tomando como origen el punto en el que querés estudiar el límite. Si por ejemplo el límite es \displaystyle \lim_{(x,y) \to (a,b)} f(x,y), podés hacer el cambio a polares como x=a+r\cos \theta, y=b+r\sin \theta. Es decir, al sumar a a la primera coordenada y b a la segunda, estás haciendo un cambio de coordenadas para que el (a,b) te quede en el origen. Una vez que trasladaste el origen, hacés el cambio a polares de siempre.

Saludos
En respuesta a Bernardo Marenco

Re: Coordenadas polares - Límites y continuidad en R^n

de Thiago Caetano Acuña Vinoles -
Ahhh claro. Y eso en la práctica, ¿es útil? ¿O se usan otros métodos para calcular límites en puntos que no sean el origen?.

Gracias por la respuesta
En respuesta a Thiago Caetano Acuña Vinoles

Re: Coordenadas polares - Límites y continuidad en R^n

de Bernardo Marenco -
Bueno, es una herramienta más para calcular límites. Otros métodos pueden ser los que vas a usar en los ejercicios 7 y 8 del práctico.

Saludos