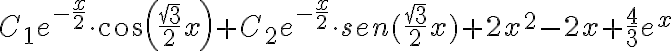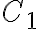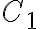Foro Práctico 2

Buenas, no se si este es el foro adecuado para consultar sobre el cuestionario pero no encontré otro.

Mi duda es sobre el siguiente ejercicio:

Lo que me complica es que las raíces del polinomio característico quedan bastate "feas": 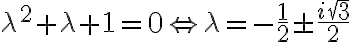$\lambda^2+ \lambda+1=0 \Leftrightarrow \lambda =- \frac{1}{2} \pm \frac{i \sqrt{3} }{2}$. Sobre todo ese 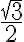$\frac{ \sqrt{3} }{2}$ que después queda dentro de seno y coseno en al solución. Y al momento de derivar y evaluar en 1 queda casi imposible de despejar las constantes.

La solución que yo llegué es: $C_1e^{- \frac{x}{2}} \cdot cos(\frac{\sqrt{3}}{2}x)+C_2e^{- \frac{x}{2}} \cdot sen(\frac{\sqrt{3}}{2}x)+2x^2-2x+ \frac{4}{3}e^x$

Agradezco me puedan ayudar!