Foro de Ejercicios fuera de los Prácticos

Hola Yliana. Podés pensarlo como un cambio de variable: como 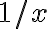$1/x$ tiende a 0 en 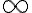$\infty$, podés pensar que estás trabajando con la función 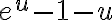$e^u -1-u$ cuando $u \to 0$ (el cambio de variable sería 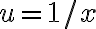$u=1/x$). Usando el desarrollo de Taylor de la exponencial en 0, llegás a que 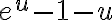$e^u -1-u$ es equivalente a 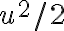$u^2/2$, que deshaciendo el cambio de variable queda $\displaystyle \frac{1}{2x^2}$.

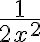Saludos