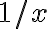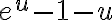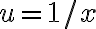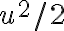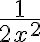CDIVV-2S: Ejemplo 3.9 3. notas cdvv (integrales impropias)

Buenas.

Estaba leyendo las notas del curso, y me tranqué en este ejemplo... No veo cómo llega a esa equivalencia. Si intento hacer el Taylor de e a la 1/x en el origen, no puedo porque las derivadas no están definidas en cero. Supongo que se referirá al Taylor de e a la x nomás, pero no comprendo porqué es correcto usar el desarrollo de esa exponencial, en lugar de la que tenemos dentro de la integral. De todas formas no consigo llegar al resultado de las notas.

Les agradezco mucho si pueden orientarme.

Re: Ejemplo 3.9 3. notas cdvv (integrales impropias)

de Bernardo Marenco - miércoles, 29 de septiembre de 2021, 09:31

Hola Yliana. Podés pensarlo como un cambio de variable: como $1/x$ tiende a 0 en $\infty$ , podés pensar que estás trabajando con la función $e^u -1-u$ cuando $u \to 0$ (el cambio de variable sería $u=1/x$ ). Usando el desarrollo de Taylor de la exponencial en 0, llegás a que $e^u -1-u$ es equivalente a $u^2/2$ , que deshaciendo el cambio de variable queda $\displaystyle \frac{1}{2x^2}$ .

Saludos