Buenas tardes, estoy leyendo la resolución de este ejercicio y no entiendo el razonamiento en general, si me pueden explicar más o menos. Tampoco entiendo por qué se toma y´ ni por qué aparece alfa.
Muchas gracias
Buenas tardes, estoy leyendo la resolución de este ejercicio y no entiendo el razonamiento en general, si me pueden explicar más o menos. Tampoco entiendo por qué se toma y´ ni por qué aparece alfa.
Muchas gracias
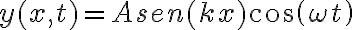 puede describir a una onda estacionaria. La respuesta es afirmativa. Una manera sencilla de verlo es porque presenta un patrón de nodos (para aquellos puntos ubicados en una posición
puede describir a una onda estacionaria. La respuesta es afirmativa. Una manera sencilla de verlo es porque presenta un patrón de nodos (para aquellos puntos ubicados en una posición  tal que
tal que 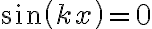 ) y antinodos (para aquellos puntos ubicados en una posición
) y antinodos (para aquellos puntos ubicados en una posición  tal que
tal que 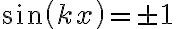 ). Y que, en particular, esta expresión permite que los extremos de la cuerda permanezcan en posiciones fijas.
). Y que, en particular, esta expresión permite que los extremos de la cuerda permanezcan en posiciones fijas. 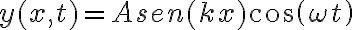 representa una onda estacionaria que correctamente puede describir la del ejercicio, ya que en el ejercicio el eje x es tal que su origen se encuentra en uno de los extremos fijos de la cuerda, por lo que se cumple la condición de borde
representa una onda estacionaria que correctamente puede describir la del ejercicio, ya que en el ejercicio el eje x es tal que su origen se encuentra en uno de los extremos fijos de la cuerda, por lo que se cumple la condición de borde 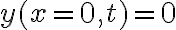 para todo tiempo (nodo en el extremo fijo). Sin embargo, en la letra se pregunta si la onda
para todo tiempo (nodo en el extremo fijo). Sin embargo, en la letra se pregunta si la onda 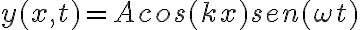 puede ser la onda estacionaria que se genera en esa cuerda de guitarra. La respuesta es que no, porque, si bien se trata de una onda estacionaria, esta no cumple la condición de borde en
puede ser la onda estacionaria que se genera en esa cuerda de guitarra. La respuesta es que no, porque, si bien se trata de una onda estacionaria, esta no cumple la condición de borde en 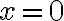 , ya que
, ya que 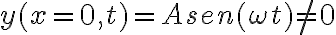 .
. que mencionás no es un alfa, sino un signo de proporcionalidad
que mencionás no es un alfa, sino un signo de proporcionalidad 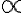 , el cual se suele utilizar cuando, para el razonamiento que estamos haciendo, no nos interesa particularmente la constante de proporcionalidad y la obviamos.
, el cual se suele utilizar cuando, para el razonamiento que estamos haciendo, no nos interesa particularmente la constante de proporcionalidad y la obviamos.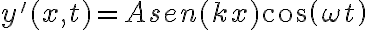 está en la solución para mostrar la forma correcta que tiene que tener la onda estacionaria para que cumpla la condición de borde en
está en la solución para mostrar la forma correcta que tiene que tener la onda estacionaria para que cumpla la condición de borde en 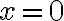 , le ponen el prima solo para diferenciarla del
, le ponen el prima solo para diferenciarla del 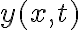 que se dio en la letra.
que se dio en la letra.