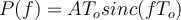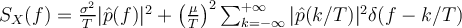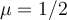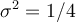SAM: Práctico 5, Ej. 3

Buenas,

Me está costando llegar a la solución y no logro entender como la misma llega al resultado.

Para calcular el SNR máximo usé que 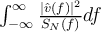$\int_{-\infty}^{\infty} \frac{\lvert \hat{v} (f) \rvert^2}{S_N (f)} df$

Si no entendí mal, 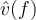$\hat{v} (f)$ es la FT del pulso rectangular que indica la letra, que debería ser 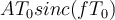$AT_0 sinc(fT_0)$ . Mi problema viene que al hacer la cuenta me da el doble del SNR que dice la solución.

Se me ocurre que esto podría ser porque solo hay 0.5 de probabilidad de que el pulso esté presente, pero en ese caso para calcular 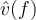$\hat{v} (f)$ tendría que transformar un proceso estocástico que no se bien como expresar.

Cualquier ayuda que me puedan dar les agradezco

Saludos,

Guillermo

Re: Práctico 5, Ej. 3

de Sergio Martínez Tagliafico - lunes, 20 de septiembre de 2021, 17:45

Efectivamente el factor 0.5 que falta en tu cálculo se debe a que la SNR que vieron con el filtro apareado se calcula cuando hay presencia de señal, no se tiene en cuanta que se envían 0's y 1's.

Para plantearlo como un proceso podes utilizar la expresión vista para la PSD de la PAM, con

$P(f) = AT_o sinc(fT_o)$ :

$S_{X}(f)=\frac{\sigma^{2}}{T}|\hat{p}(f)|^{2}+\left(\frac{\mu}{T}\right)^{2} \sum_{k=-\infty}^{+\infty}|\hat{p}(k / T)|^{2} \delta(f-k / T)$

como estas transmitiendo 0's y 1's de forma equiproblable tenes que

$\mu = 1/2$ y

$\sigma^2 = 1/4$ .