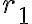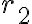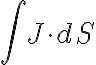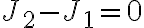Buenas me surgió una duda al resolver la parte a)ii de este problema, para resolver la parte anterior usé la hipótesis de que estamos en régimen estacionario, por lo que la divergencia de 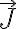 es nula, por ende podemos utilizar la ecuación de Laplace para hallar el potencial electrostático y luego el campo eléctrico, pero luego para hallar la resistencia primero necesito la corriente, la cual calculo a partir del flujo de
es nula, por ende podemos utilizar la ecuación de Laplace para hallar el potencial electrostático y luego el campo eléctrico, pero luego para hallar la resistencia primero necesito la corriente, la cual calculo a partir del flujo de 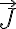 utilizando una esfera de radio fijo
utilizando una esfera de radio fijo 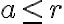 y
y 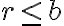 , pero mi duda está en por que este flujo no es nulo? ya que aplicando el teorema de la divergencia obtendríamos
, pero mi duda está en por que este flujo no es nulo? ya que aplicando el teorema de la divergencia obtendríamos 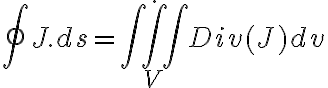 , y como estamos en régimen estacionario esto daria 0, por que estaría mal el razonamiento? Desde ya muchas gracias
, y como estamos en régimen estacionario esto daria 0, por que estaría mal el razonamiento? Desde ya muchas gracias
Se entendió perfecto, me estaba mareando con el volumen si, muchas gracias!
Buenas, una consulta, en la parte (d), pide hallar la resistencia con la relacion RC y luego dice "Compare con el Problema Nº 3 del práctico 2", pero en ese problema se halla la capacitancia, por lo que supongo que se refiere a que utilicemos el C de ese ejercicio para hallar R, ¿Es correcto?, y otra duda, en estos ejercicios estoy utilizando Laplace para hallar el campo electrico y luego la densidad volumetrica, entiendo que funciona, pero capaz que estos ejercicios estan orientados a resolverlos de otra forma, pregunto por si acaso.
Saludos
Diego
Saludos
Diego
es correcto, sabiendo la relacion de RC con las constantes microscopicas (conductividad y permitividad), podes usar C para hallar R.
Tambien es correcto el procedimiento, que se basa en que no hay densidad volumetrica de carga libre ni variacion con el tiempo, por ende se puede justificar div de E nula.
Tambien es correcto el procedimiento, que se basa en que no hay densidad volumetrica de carga libre ni variacion con el tiempo, por ende se puede justificar div de E nula.