Foro Práctico 6

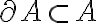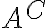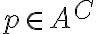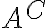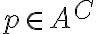Hola, hay una forma más directa de probarlo sin usar esa propiedad: tomemos un conjunto $A$ tal que $\partial A \subset A$ y supongamos que $A$ no es cerrado, es decir, que $A^C$ no es abierto. Esto implica que existe un punto $p\in A^C$ que no es interior a $A^C$, o sea que toda bola centrada en $p$ contiene al menos un punto de $A$. Formalmente, existe un $p\in A^C$ tal que para todo radio 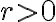$r>0$ la bola 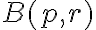$B(p,r)$ cumple 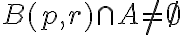$B(p,r) \cap A \neq \emptyset$. 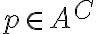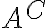Como $p\in A^C$, esto quiere decir que toda bola centrada en $p$ interseca tanto a $A$ como a $A^C$, es decir, que $p$ es un punto frontera de $A$. Entonces encontramos un punto frontera de $A$ que no pertenece a $A$ (ya que pertenece a 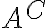$A^C$), lo que contradice la hipótesis que $\partial A \subset A$.

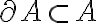Saludos