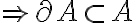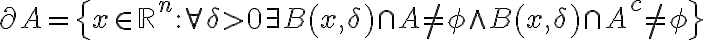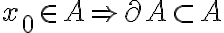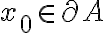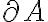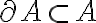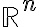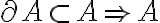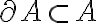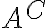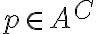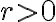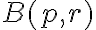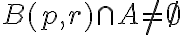Ejercicio 6.c

Ejercicio 6.c

de Joel Cabrera Dechia -
Número de respuestas: 4

Buenas, como va?

Estoy intentando las demostraciones; me pasa en general que leo las hipótesis y a lo que tengo que llegar y me parece trivial pero al momento de demostrar colapso, así que agradezco si me pueden tirar algún pique si pifie en algo acá, por donde encararlo mejor, correcciones generales, etc.

A es cerrado  \Rightarrow \partial A\subset A

Por definición sabemos que  \partial A=\{ x\in \mathbb{R} ^{n}:\forall \delta >0\exists B\left( x,\delta \right) \cap A\neq \phi \wedge B\left( x,\delta \right) \cap A^{c}\neq \phi \}

Tomo un  x_{0}\in \partial A  
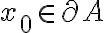
Supongo por absurdo que 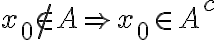 x_{0}\notin A\Rightarrow x_{0}\in A^{c}

Como A es cerrado 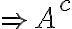 \Rightarrow A^{c} es abierto por lo que  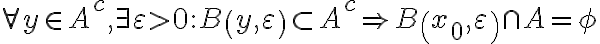\forall y\in A^{c},\exists \varepsilon >0:B\left( y,\varepsilon \right) \subset A^{c}\Rightarrow B\left( x_{0},\varepsilon \right) \cap A=\phi pero eso es absurdo por definición de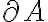  \partial A

De ahí concluyo que pertenece a A pero no sé cómo concluir toda la demostración.

Tengo una duda a partir de esto: ¿si un elemento no pertenece a un conjunto entonces pertenece a su complemento? Yo para la demostración lo di por válido pero capaz no se cumple.

Saludos.
En respuesta a Joel Cabrera Dechia

Re: Ejercicio 6.c

de Joel Cabrera Dechia -
Quizás ya directamente para concluir puedo decir que como x_{0}\in A\Rightarrow \partial A\subset A
Pero me suena raro.
En respuesta a Joel Cabrera Dechia

Re: Ejercicio 6.c

de Bernardo Marenco -
Hola Joel, está perfecta la prueba. Efectivamente la conclusión es la que decís: como el  x_0\in \partial A que tomaste es genérico, lo que probaste es que cualquier punto en \partial A también está en A, es decir, que \partial A\subset A. Algo interesante a notar es que tu prueba funciona aunque el espacio no sea \mathbb{R}^n, con que haya una noción de distancia te alcanza (o sea que esto vale para cualquier espacio al que le puedas poner una distancia).

Ahora lo que te falta es probar la otra dirección del si y sólo si (Si \partial A\subset A \Rightarrow A es cerrado).

Saludos
En respuesta a Bernardo Marenco

Re: Ejercicio 6.c

de Joel Cabrera Dechia -
Hola Bernardo, muchas gracias por tu respuesta!
Para demostrar el otro lado, puedo simplemente usar la propiedad de que A es cerrado sii contiene a todos sus puntos de acumulación? Porque estos son los que la bola reducida interseca a A, y en la hipótesis tengo que la frontera está incluida en A, y por definición de frontera pertenecen a esta los puntos que intersecan a A.

No se si puedo usar la propiedad porque justamente después el ejercicio me pide demostrar eso mismo. Quizás si lo demuestro primero luego puedo usarlo, pero quizás hay alguna otra forma de demostrar lo anterior sin usar la propiedad.

Saludos
En respuesta a Joel Cabrera Dechia

Re: Ejercicio 6.c

de Bernardo Marenco -

Hola, hay una forma más directa de probarlo sin usar esa propiedad: tomemos un conjunto A tal que \partial A \subset A y supongamos que A no es cerrado, es decir, que A^C no es abierto. Esto implica que existe un punto p\in A^C que no es interior a A^C, o sea que toda bola centrada en p contiene al menos un punto de A. Formalmente, existe un p\in A^C tal que para todo radio r>0 la bola B(p,r) cumple B(p,r) \cap A \neq \emptyset. Como p\in A^C, esto quiere decir que toda bola centrada en p interseca tanto a A como a A^C, es decir, que p es un punto frontera de A. Entonces encontramos un punto frontera de A que no pertenece a A (ya que pertenece a A^C), lo que contradice la hipótesis que \partial A \subset A.

Saludos