Hola. Sobre la pregunta 1: tu razonamiento está perfecto, la afirmación es verdadera. Es el cuestionario el que está mal, ya lo corregí.
Sobre la pregunta 2: para ver que la afirmación (I) es falsa basta dar un contraejemplo. Puede ser  y
y 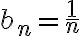 . Ahí
. Ahí 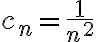 , entonces su serie converge pero la de
, entonces su serie converge pero la de 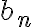 no.
no.
Para ver que las afirmaciones (II) y (III) son verdaderas, fijate que 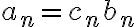 . Si
. Si 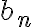 está acotada, entonces existe un
está acotada, entonces existe un 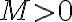 tal que
tal que 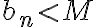 , por lo que
, por lo que 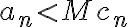 . Si la serie de
. Si la serie de 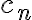 converge, entonces la serie de
converge, entonces la serie de 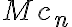 también lo hace. Luego la serie de
también lo hace. Luego la serie de  converge por comparación. Para probar (III) podés hacer algo parecido con
converge por comparación. Para probar (III) podés hacer algo parecido con 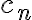 : si la sucesión
: si la sucesión 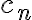 converge, entonces está acotada por un
converge, entonces está acotada por un 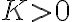 . Por lo tanto
. Por lo tanto 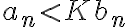 y podés volver a usar comparación.
y podés volver a usar comparación.
Saludos
