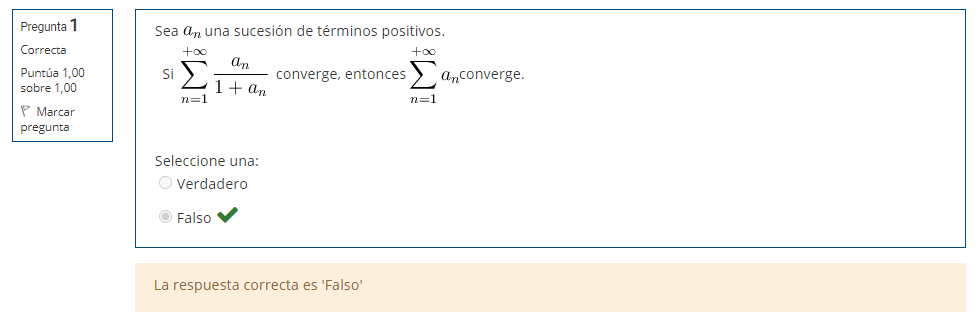
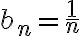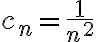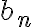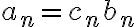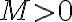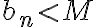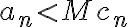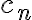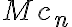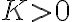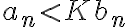Hola, para el ejercicio 1 adjunto como lo pensé yo, llego a que es verdadera la afirmación, hay algo que razoné mal pues la respuesta correcta es falsa, quisiera saber si pueden indicarme que fue.
Y en el ejercicio 2 agradecería si pudieran darme una mano ya que me entrevere y no se como hacerlo.
Muchas gracias