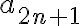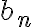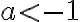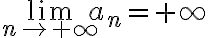Muchas gracias! Quedo claro.
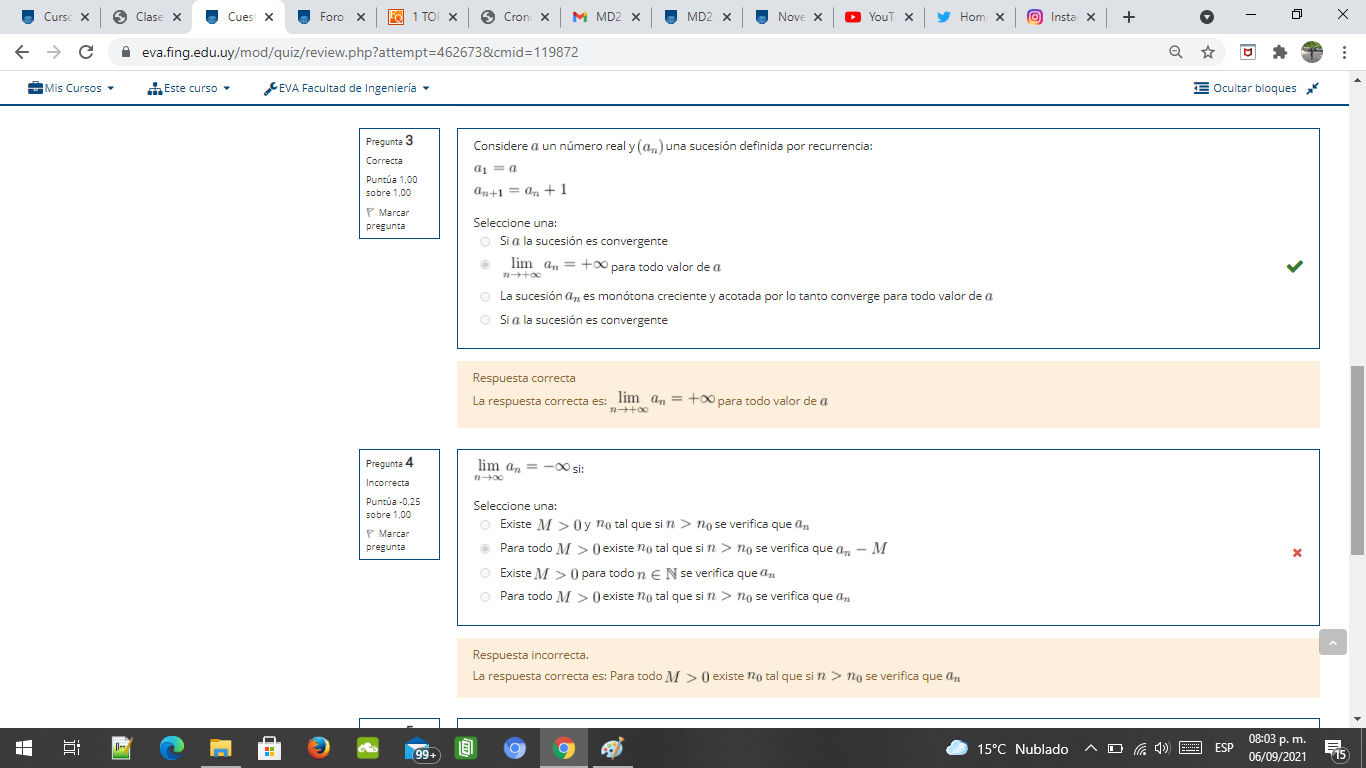
Ahora tengo otra consulta sobre otro ejercicio, la opción correcta de este ejercicio indica que si a<-1, supongamos que a=-2, la sucesión nos queda de la forma -2, 4, 16, 256, etc, cuando n tiende a +infinito el limite de la sucesión es +infinito ¿Esto seria que no existe el limite? y después, como definición de sucesión acotada inferiormente tengo lo siguiente: an esta acotada inferiormente si Existe m perteneciente a los Reales tal que m<= an para todo n perteneciente a los Naturales, entonces no entiendo por que la sucesión no estaría acotada inferiormente, agradezco si puedes aclarármelo ya que no logre llegar a ninguna de las opciones