Hola, estuve varios días tratando de resolver este ejercicio y no pude. La parte a) la pude resolver sin problema y llegué al resultado correcto. Sin embargo, no se cómo resolver la parte b. Trate hacer la integral entre 0 y srqt(a.b) de U/V dV pero no estoy seguro sobre el volumen que tengo que divir y cuál sería la expresión de dV. Yo tomé V = π.(b^2).h y dV = π.h.r.dr
Hola, vos estas tratando de probar que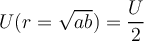 
para eso necesitas la energ'ia total almacenada en el capacitor y calcular la energ'ia almacenada en un cilindro con ese radio.
Acordate que la energia almacenada puede escribirse como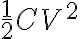
y que V lo podes calcular teniendo el campo, vas a necesitar acordarte tambien de la regla de la potencia y la division en los logaritmos y avivarte de que 
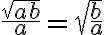, te digo esto ultimo por que me llev'o un ratito darme cuenta a mi.
Si esta respuesta no es suficientemente clara por favor volv'e a consultar.
Saludos!
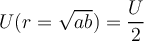para eso necesitas la energ'ia total almacenada en el capacitor y calcular la energ'ia almacenada en un cilindro con ese radio.Acordate que la energia almacenada puede escribirse como
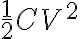y que V lo podes calcular teniendo el campo, vas a necesitar acordarte tambien de la regla de la potencia y la division en los logaritmos y avivarte de que 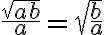, te digo esto ultimo por que me llev'o un ratito darme cuenta a mi.Si esta respuesta no es suficientemente clara por favor volv'e a consultar.
Saludos!
Trato de nuevo con las ideas que me planteaste. Si sigo sin entender vuelvo a consultar, gracias!