Estuve viendo el ejercicio que no salia hoy y ya entendi que paso, paso a detallar:
Por un lado cuando encontramos los valores propios 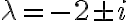 nos queda que la matriz
nos queda que la matriz  la cual es semejante a
la cual es semejante a  es
es
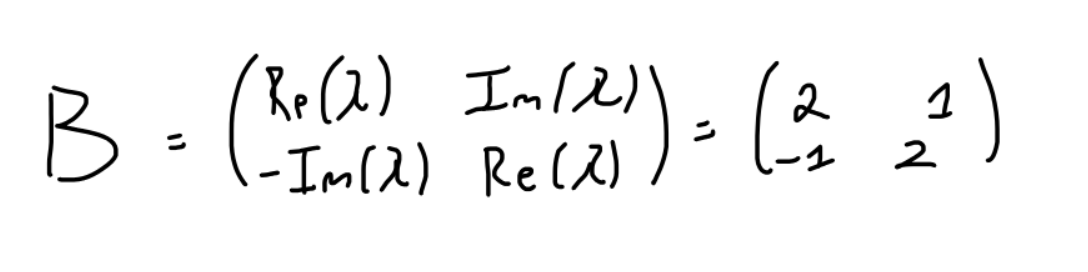
Por otro lado, el vector propio hallado 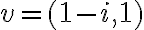 nos da la matríz
nos da la matríz  siguiente:
siguiente:
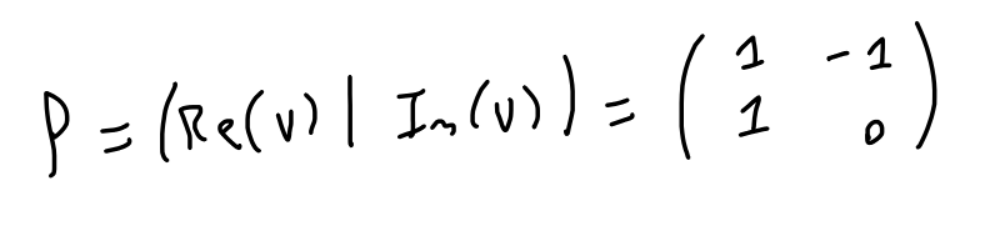
Lo de la matriz 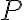 lo pueden leer en la página 11 de las notas 3.
lo pueden leer en la página 11 de las notas 3.
Finalmente la solución 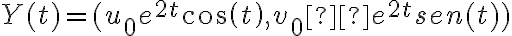 donde
donde 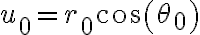 y
y 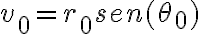 .
.
Luego a partir de la condición inicial 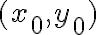 podemos encontrar
podemos encontrar 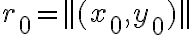 y
y 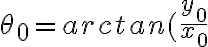 . Para esto último es útil hacer un dibujito para convencerse.
. Para esto último es útil hacer un dibujito para convencerse.
Cualquier cosa la que viene lo volvemos a mirar, saludos!
