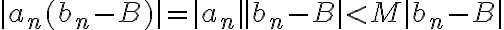Foro Práctico 3

Hola Pablo. Está bien la idea de la demostración. Tiene solo un detalle: no se puede aplicar la definición de convergencia de 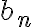$b_n$ con ese 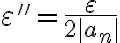$\displaystyle \varepsilon''=\frac{\varepsilon}{2|a_n|}$. En la definición de límite el 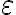$\varepsilon$ tiene que ser un número real, no puede depender de $n$. Ahí lo que podés usar es que si $a_n$ es convergente, entonces está acotada. Por lo tanto, existe un 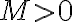$M>0$ tal que 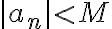$|a_n| < M$. Entonces:

$|a_n(b_n-B)|= |a_n||b_n-B| < M|b_n-B|$.

Ahora si, podés tomar 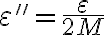$\displaystyle \varepsilon''=\frac{\varepsilon}{2M}$ para usar la definición de convergencia de $b_n$.

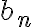Saludos