Hola,
Es cierto que ninguna solución de la primera inecuación puede ser menor a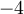 (de lo contrario
(de lo contrario 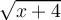 no queda definido, como bien decís). Te faltó observar que una solución de esta inecuación tampoco puede ser menor a cero, de lo contrario tendrías algún
no queda definido, como bien decís). Te faltó observar que una solución de esta inecuación tampoco puede ser menor a cero, de lo contrario tendrías algún 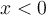 que además cumple
que además cumple 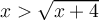 . Como
. Como 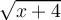 es positivo (o cero) para cualquier
es positivo (o cero) para cualquier  donde esté definida, las dos condiciones son incompatibles.
donde esté definida, las dos condiciones son incompatibles.
Es por esto que se descartaron los valores negativos. Resultan ser soluciones ficticias (aparecieron al elevar al cuadrado).
Espero aclare,
Saludos
Es cierto que ninguna solución de la primera inecuación puede ser menor a
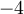 (de lo contrario
(de lo contrario 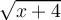 no queda definido, como bien decís). Te faltó observar que una solución de esta inecuación tampoco puede ser menor a cero, de lo contrario tendrías algún
no queda definido, como bien decís). Te faltó observar que una solución de esta inecuación tampoco puede ser menor a cero, de lo contrario tendrías algún 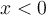 que además cumple
que además cumple 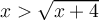 . Como
. Como 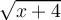 es positivo (o cero) para cualquier
es positivo (o cero) para cualquier  donde esté definida, las dos condiciones son incompatibles.
donde esté definida, las dos condiciones son incompatibles.Es por esto que se descartaron los valores negativos. Resultan ser soluciones ficticias (aparecieron al elevar al cuadrado).
Espero aclare,
Saludos
