Hola buenas, yo llegué al resultado del ejercicio usando una la ecuación de la foto, esa ecuación contiene el parámetro n, y yo lo tomé como n=1 ¿Me dirían por arriba que es la teoría que hay detrás?
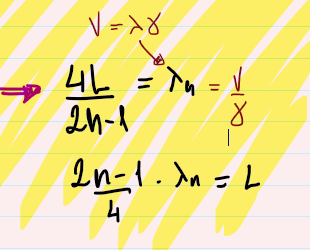
Hola buenas, yo llegué al resultado del ejercicio usando una la ecuación de la foto, esa ecuación contiene el parámetro n, y yo lo tomé como n=1 ¿Me dirían por arriba que es la teoría que hay detrás?
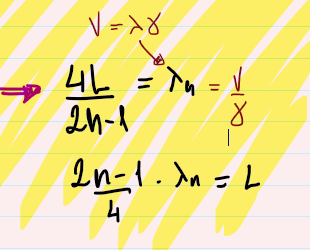
Cuando tenes un extremo libre y uno fijo la primera estacionaria se da cuando, al ajustar la frecuencia, el largo del tubo es un cuarto de lambda. Si aumentas la frecuencia el próximo modo estacionario se da cuando en el largo del tubo entre media más un cuarto de lambda (o sea tres cuartos de lamda es el largo del tubo). Así el lambda de cada estacionaria tiene que cumplir que el largo sea número impar de cuartas lambdas.
 .
.  .
.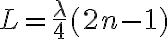
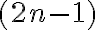 siempre da impar.
siempre da impar.