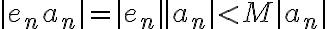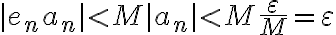CDIVV-2S: Ejercicio 2d

Hola, tenía dudas sobre como encarar este ejercicio y al ir a buscar su demostración en las notas que nombra la solución (también busqué en las de Marco Pérez), vi que allí tampoco está realizado y se deja como ejercicio. Cómo me recomiendan encararlo? Intenté replicar alguna de las ideas de las demostraciones anteriores pero al no saber si la sucesión e converge o no, no logré plantear ninguna desigualdad más allá de su acotación. Gracias!

Re: Ejercicio 2d

de Bernardo Marenco - jueves, 19 de agosto de 2021, 10:55

Hola Ivana. Para probar que 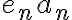$e_n a_n$ tiende a 0 deberías probar que para todo 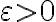$\varepsilon >0$ existe un 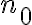$n_0$ tal que para todo 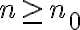$n\geq n_0$ se cumple 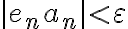$|e_n a_n|< \varepsilon$ (dicho en palabras, que a partir de cierto momento podés hacer a 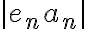$|e_n a_n|$ tan chico como vos quieras). Como 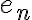$e_n$ está acotada entonces existe un real 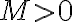$M>0$ tal que 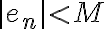$|e_n| < M$ para todo $n$ , así que podemos escribir:

$|e_n a_n| = |e_n||a_n| < M|a_n|$

Intuitivamente, como 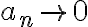$a_n \to 0$ podemos hacer a 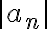$|a_n|$ tan chico como querramos, por lo que podemos hacer al producto 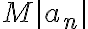$M|a_n|$ tan chico como querramos. Formalmente, como 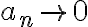$a_n \to 0$ existe un 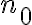$n_0$ a a partir del cual 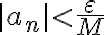$\displaystyle|a_n| < \frac{\varepsilon}{M}$ . Entonces para todo $n$ mayor o igual que ese $n_0$ :

$\displaystyle |e_n a_n| < M|a_n| < M \frac{\varepsilon}{M} = \varepsilon$

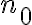probando lo que queremos.

Saludos