Prog3: Ejercicio 2.b del practico de la semana 2

Buenas,

El ejercicio plantea la siguiente pregunta : El hecho que acaba de demostrar en la parte (a), ¿depende de la implementación específica del algoritmo de Gale-Shapley que consideremos? Justifique. En la parte a se demostró que G-S es Ω(n^2)

Cual es la respuesta y por que? Supongo que la respuesta es que no depende ya que en el peor caso el numero de propuestas es de orden n^2 y eso es independiente de como se implemente, pero no estoy 100% seguro de que sea así y si lo es, tampoco se me ocurre como demostrarlo mas formalmente

Muchas gracias.

Re: Ejercicio 2.b del practico de la semana 2

de Sofia Tito Virgilio Rodriguez - lunes, 16 de agosto de 2021, 19:19

Hola Tomas.

Efectivamente la respuesta es que no depende porque existe al menos una instancia del problema en la que el número de propuestas es 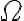$\Omega$ (n²) independientemente de la implementación.

Lo que es necesario justificar es por qué el número de propuestas es independiente de la implementación, en particular, ¿por qué no depende del orden en el que se selecciona al siguiente hombre libre?.

La justificación viene por el lado de que el emparejamiento estable obtenido por el algoritmo de G-S para esa instancia del problema es siempre el mismo (S*) independientemente de la implementación.

Por lo tanto, para cualquier implementación, tras ejecutar G-S sobre la instancia del problema presentada en la parte a) un hombre m siempre va a terminar emparejado con su mejor pareja válida w.

Además, la cantidad de propuestas que ese hombre m tiene que hacer para terminar emparejado con la mujer w también es independiente de la implementación, ya que siempre tiene que realizarle una propuesta a todas las mujeres que están antes que w en su lista de preferencias, y una propuesta a w.

Como esto se cumple para todos los hombres, tenemos que la cantidad total de propuestas que realizan los hombres antes de llegar a sus parejas definitivas es independiente de la implementación y por lo tanto es 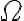$\Omega$ (n²) como se vio en la parte a) del ejercicio.

Como además cada iteración del algoritmo lleva al menos tiempo 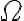$\Omega$ (1), concluimos que el tiempo de ejecución es 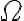$\Omega$ (n²) independientemente de cómo se implemente el algoritmo.

No sé si quedó un poco más claro, cualquier cosa lo seguimos viendo.

Saludos!

Re: Ejercicio 2.b del practico de la semana 2

de Tomas Pasacual Sexenian Lopez - viernes, 20 de agosto de 2021, 12:41

Entiendo que el loop while es el que es de orden n² y como lo que esta dentro de el (encapsulado en rojo) es de orden O(1) es que se deduce el tiempo $\Omega$ (n²).

Lo que todavía no termino de entender es el hecho de que el bloque rojo es de tiempo O(1) independientemente de como se implemente. No podría trabajar con listas en lugar de arreglos para hacer que el bloque tarde mas tiempo en iterar? Suponer que para saber si w está libre llevo una lista simplemente enlazada de mujeres libres o que las parejas comprometidas también son representadas en una lista y yo inserto (m,w) siempre al final ?

Re: Ejercicio 2.b del practico de la semana 2

de Sofia Tito Virgilio Rodriguez - viernes, 20 de agosto de 2021, 14:00

Hola Tomas.

El bloque rojo no es O(1), es

$\Omega$ (1), es decir, que voy a invertir al menos tiempo constante en cada iteración del while.

Dependiendo de la implementación podría llegar a invertir más tiempo por iteración, pero la cota inferior

$\Omega$ (1) se sigue cumpliendo.

Como en peor caso voy a iterar del orden de n²veces invirtiendo al menos un tiempo constante en cada iteración, entonces en peor caso el while me va a llevar al menos un tiempo del orden de n², que es la noción de

$\Omega$ (n²), acotar inferiormente el comportamiento del tiempo de ejecución de mi algoritmo.

Luego puedo encontrar una implementación que me permita alcanzar esa cota inferior, o puedo encontrar otras implementaciones que no puedan alcanzarla e inviertan un tiempo de orden mayor en cada iteración del algoritmo (por ejemplo usando listas), pero nunca voy a encontrar una implementación que me permita invertir un tiempo de orden menor en cada iteración, por lo que la cota inferior sobre el tiempo de ejecución del peor caso se cumple para toda implementación.

Avisame si ahora quedó un poco más claro, sino lo seguimos viendo.

Saludos!