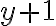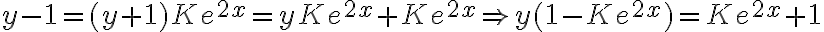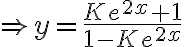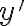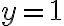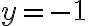Ejercicio 1, a

Ejercicio 1, a

de Julian Pastoriza Gutierrez -
Número de respuestas: 5
Hola, llegué a un punto del ejercicio 1.a. que no sé como seguir, y ademas tengo una consulta sobre la solución general de la ecuación diferencial.

Luego de separar las variables (y2 -1) y 1, las integré y usando fracciones simples llegué a un resultado de la forma 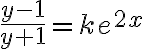 \frac{y-1}{y+1} = ke^{2x} , donde k es una constante.

Lo que no sé es si se puede despejar y del resultado, ni si esta es la solucion general de la ecuación o tengo que hacer algo más para hallarla.

Gracias!
En respuesta a Julian Pastoriza Gutierrez

Re: Ejercicio 1, a

de Bernardo Marenco -

Hola Julián. Llegaste bien a la igualdad, ahora lo que te falta es despejar y. Podés pasar multiplicando el y+1 del denominador y juntar todo lo que tiene y de un lado y todo lo que no tiene y del otro:

\displaystyle y-1 = (y+1)Ke^{2x} = yKe^{2x} + Ke^{2x} \Rightarrow y(1-Ke^{2x}) = Ke^{2x}+1

\displaystyle \Rightarrow y = \frac{Ke^{2x}+1}{1-Ke^{2x}}

Saludos
En respuesta a Bernardo Marenco

Re: Ejercicio 1, a

de Julian Pastoriza Gutierrez -
Ah era bastante fácil jeje, gracias Bernardo.

Y no me queda claro si esas son todas las soluciones de la ecuación diferencial, podrías aclararmelo?
En respuesta a Julian Pastoriza Gutierrez

Re: Ejercicio 1, a

de Bernardo Marenco -
Esas no son todas las soluciones: faltan las soluciones constantes, que se hallan igualando y' a 0 (justamente, porque son constantes). En este caso son y=1 e y=-1.

Saludos
En respuesta a Bernardo Marenco

Re: Ejercicio 1, a

de Liber Maximiliano Falco Gomez -


Bernardo, quería consultarte respecto a la observación que plantean en el pdf de las soluciones respecto a este ejercicio. En concreto sobre el valor de la constante C, que entiendo de donde sale (haciendo cuentas con la solución) pero no logro intepretar su significado.