MI- 2S: Ejercicio 2, problema 16

Como se realiza este? No puedo hacerlo

Re: Ejercicio 2, problema 16

de Alberto Marcelo Camirotte Foliadoso - jueves, 12 de agosto de 2021, 10:18

Hola Gonzalo.
La ecuación esta es una polinómica de tercer grado que tiene una solución "evidente".
Observamos que los coeficiente: 1, -3, 3 y 1 suman 0. Entonces x=1 es solución de la ecuación.

Una vez que conocemos una solución de la ecuación podemos encontrar, si las tiene, las otras soluciones.

Como x=1 es solución, entonces:

$x^3 - 3x^2 + 3x -1 = (x-1) (ax^2+bx+c)$

Lo que tenemos que hacer ahora es encontrar el factor

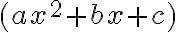
$(ax^2 + bx +c)$ , para esto vamos a dividir

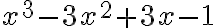
$x^3-3x^2+3x-1$ entre

$(x-1)$

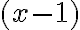
Esta división la podemos hacer usando el esquema de Ruffini:

$\begin{tabular}{c|c|c|c|c|c} & 1 & -3 & 3 &-1 \\ \hline 1 & & 1 & -2 & 1 & \\ \hline & 1 & -2 & 1 & 0 \\ \end{tabular}$

Luego el factor

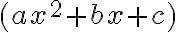
$(ax^2 + bx +c)$ es

$(x^2 -2 x +1)$

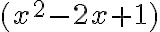
Por lo tanto:

$x^3 - 3x^2 + 3x -1 = (x-1) (x^2-2x+1)$

Entonces las restantes soluciones de la ecuación, en caso de existir, provienen de resolver

$x^2-2x+1=0$ .

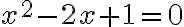
Espero haber aclarado.

Saludo!