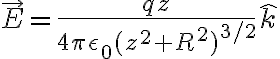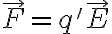Hola,
No entiendo bien lo que hiciste en la hoja que adjuntas, así que te voy a dar unas ideas de como encarar el ejercicio.
Sea 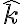 un versor vertical (perpendicular al plano del circulo cargado). Entonces, en la parte a) se obtiene que el campo eléctrico a lo largo del eje del circulo es de la forma
un versor vertical (perpendicular al plano del circulo cargado). Entonces, en la parte a) se obtiene que el campo eléctrico a lo largo del eje del circulo es de la forma
Aca  es la coordenada que mide la distancia del plano del aro a lo largo del eje. Tomamos
es la coordenada que mide la distancia del plano del aro a lo largo del eje. Tomamos  creciente en la direccion de
creciente en la direccion de 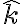 . Cuando tenes una particula con carga
. Cuando tenes una particula con carga 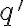 en presencia de un campo el'ectrico
en presencia de un campo el'ectrico 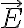 , entonces la fuerza sobre la particula es de la forma
, entonces la fuerza sobre la particula es de la forma
En este caso ten'es una particula de carga 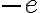 sobre el eje, enconces la fuerza que experimenta la part'icula es de la forma
sobre el eje, enconces la fuerza que experimenta la part'icula es de la forma

Ahora las observaciones clave son: 1) La fuerza sobre la particula se anula en 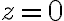 , por lo que entonces esta es una posicion de equilibrio del movimiento de la particula. 2) Como e>0 y ademas q>0 por letra, entonces para pequenios deplazamientos del equilibrio, es decir para
, por lo que entonces esta es una posicion de equilibrio del movimiento de la particula. 2) Como e>0 y ademas q>0 por letra, entonces para pequenios deplazamientos del equilibrio, es decir para 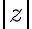 chicos, la fuerza tiende a devolver a la particula al equilibrio. Es decir que si moves a la particula una distancia corta en la direccion de
chicos, la fuerza tiende a devolver a la particula al equilibrio. Es decir que si moves a la particula una distancia corta en la direccion de 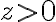 la fuerza es opuesta a
la fuerza es opuesta a 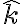 y cuando moves la part una distancia corta en la direccion
y cuando moves la part una distancia corta en la direccion  la fuerza es segun
la fuerza es segun 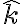 . Verifica esto por tu cuenta.
. Verifica esto por tu cuenta.
De las consideraciones anteriores podemos deducir entonces que para 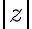 chico la fuerza es aproximadamente de la forma
chico la fuerza es aproximadamente de la forma
![]()
Podes verificar esto haciendo un desarrollo de Taylor a primer orden de la expresi'on de la fuerza alrededor de 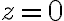 . Haciendo eso vas a hallar
. Haciendo eso vas a hallar  y verificar que
y verificar que 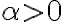 .
.
De esto vemos que la ecuaci'on de Newton para la particula para  chico es de la forma
chico es de la forma
![]()
Esta es la ecuaci'on de un oscilador armonico. De esta ecuacion podes deducir cual es la frecuencia de oscilaci'on.
Espero que esto te sirva, de lo contrario no dudes en volver a preguntar
Saludos
G