GAL2-1S: ej examen 17/7

Hola quería saber porque esta afirmación es falsa ya que no me queda claro

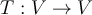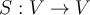Sean $T:V\to V$ y $S:V\to V$ dos operadores autoadjuntos, entonces 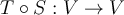$T\circ S:V\to V$ es un operador autoadjunto

Dado el teorema espectral para operadores autoadjuntos. V e.v. sobre K de dimensión finita T : V → V operador autoadjunto ⇒ existe base ortonormal formada por vep en particular, T es diagonalizable

Matriz(ToS)=Matriz(T).Matriz(S) en las bases dadas por sus veps

Osea si existe su forma diagonal entonces el producto de matrices no seria daigonal ?

¿Mi error estaria en que aunque el producto de matrices quede diagonal y por tanto simetrica ,la base de dicha matriz no seria ortonormal por lo tanto no seria autoadjunta? Pero las bases son foradas por veps y bon entonces no me queda claro

gracias de antemano

Re: ej examen 17/7

de Bruno Tadeo Cardozo Pintos - domingo, 18 de julio de 2021, 23:01

Hola, no se si te sirva mi respuesta pero, tengo entendido que la composición de autoadjuntos es autoadjunto si y sólo si T y S conmutan. Es una de las propiedades que piden demostrar en el práctico 9, ejercicio 2.

Re: ej examen 17/7

de Ana González - lunes, 19 de julio de 2021, 12:41

Buenas tardes.
Lo que dice Bruno es el problema con la afirmación de ese ejercicio. Si los operadores no conmutan la composición de operadores autoadjuntos no va a ser autoadjunta.
En el razonamiento de Nahuel el problema está en que las bases ortonormales de vectores propios de cada operador no tiene porque ser la misma. Por lo tanto no se puede hacer el razonamiento que se detalla.
Es muy fácil construir contraejemplos a esa afirmación. Basta tomar, por ejemplo, dos matrices reales simétricas cuyo producto no conmute.
Espero esto ayude a entender como resolver el ejercicio.
Saludos