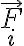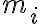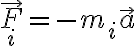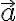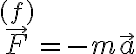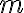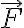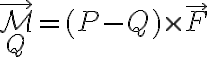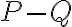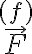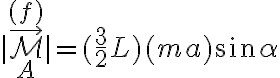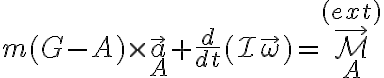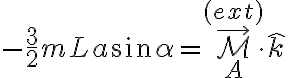Foro de consultas generales

Hola, Alejo. Tu pregunta es interesante, porque de hecho se puede resolver el ejercicio de formas diferentes. ¿Pudiste llegar a un resultado?

(1) Pseudo fuerza:

En la solución publicada usan la astucia de plantear la segunda cardinal en un sistema de referencia no inercial, con respecto al cual el centro de masas está en reposo y el cuerpo no rota.

Se puede demostrar que esto equivale a considerar el sistema relativo como si fuera inercial, pero agregando una fuerza adicional 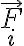$\vec F_i$ sobre cada partícula 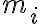$m_i$, de valor 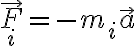$\vec F_i=-m_i \vec a$, siendo 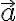$\vec a$ la aceleración producida por el sistema relativo (transporte+Coriolis). A esta fuerza se le llama fuerza ficticia o pseudo-fuerza (trata de demostrar esta propiedad en unos dos o tres renglones).

A su vez, como en este caso la aceleración 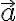$\vec a$ es la misma para todas las partículas, el efecto neto de la fuerza ficticia es equivalente a una fuerza 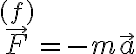$\vec F^{(f)} = -m \vec a$ aplicada en el centro de masas del sistema (cuerpo), siendo 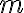$m$ la masa total. La demostrar es completamente análoga al caso de la fuerza peso (no estaría mal repasar esta demostración).

(2) Momento de la pseudo-fuerza:

Para encontrar el momento (torque) producido por cada fuerza 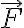$\vec F$ con respecto a un punto Q hay que calcular el producto vectorial

$\vec {\mathcal {M}}_Q = (P-Q) \times \vec F$

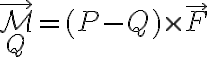
siendo P el punto de aplicación de la fuerza, y 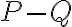$P-Q$ es el vector que va de P a Q. En el caso del momento que preguntas, la fuerza ficticia 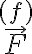$\vec F^{(f)}$ es horizontal (opuesta al versor i) aplicada en P=G (centro de masas), Q=A es el punto de la articulación, y el vector de posición forma un ángulo $\alpha$ con la horizontal. El módulo del momento correspondiente resulta

$|\vec {\mathcal {M}}^{(f)}_A|=(\frac 3 2 L) (m a) \sin \alpha$

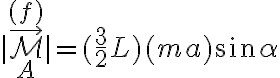
y el vector es saliente al dibujo. Por lo tanto, aunque la aceleración de la barra es horizontal, en el sistema relativo la pseudo-fuerza produce un momento no nulo con respecto al punto A.

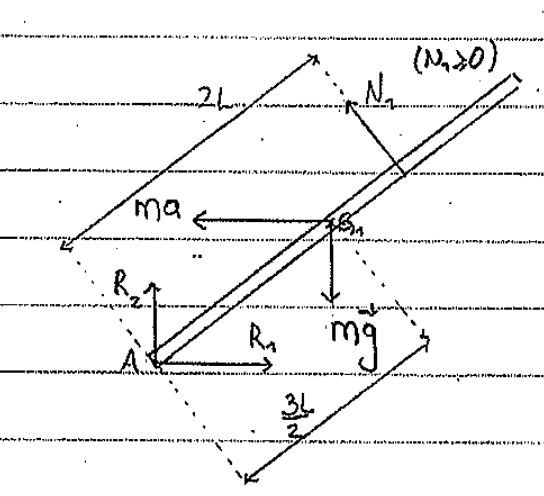
(3) Segunda Cardinal en el sistema inercial (otro planteo):

Una alternativa para plantear el ejercicio es usar la forma de la segunda cardinal en el sistema inercial (en el cual cada punto la barra tiene aceleración 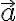$\vec a$). Con respecto al punto A (que pertenece a la barra) se obtiene

$m(G-A)\times \vec a_A + \dfrac {d}{dt}(\mathcal{I} \vec \omega) = \vec {\mathcal {M}}^{(ext)}_A$

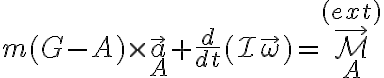
(revisa la deducción en el capítulo 8 de las notas del teórico). Esta vez, en el momento externo solo se incluyen los que producen las fuerzas reales.

Como la barra se encuentra en equilibrio relativo, el segundo término en el lado izquierdo es cero porque las derivadas temporales se anulan. Calculando el producto vectorial (queda entrante al dibujo) y proyectando según k (saliente al dibujo) se obtiene

$-\frac{3}{2} m L a \sin \alpha = \vec {\mathcal{M}}^{(ext)}_A \cdot \hat k$

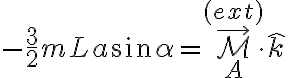
que es la misma ecuación que en el otro método, si pasamos todos los términos para un mismo lado.

--------------------------

Espero que se haya aclarado el panorama y te hayas entretenido. No dudes en escribir de nuevo si quieres seguir discutiendo.

Saludos,
NC