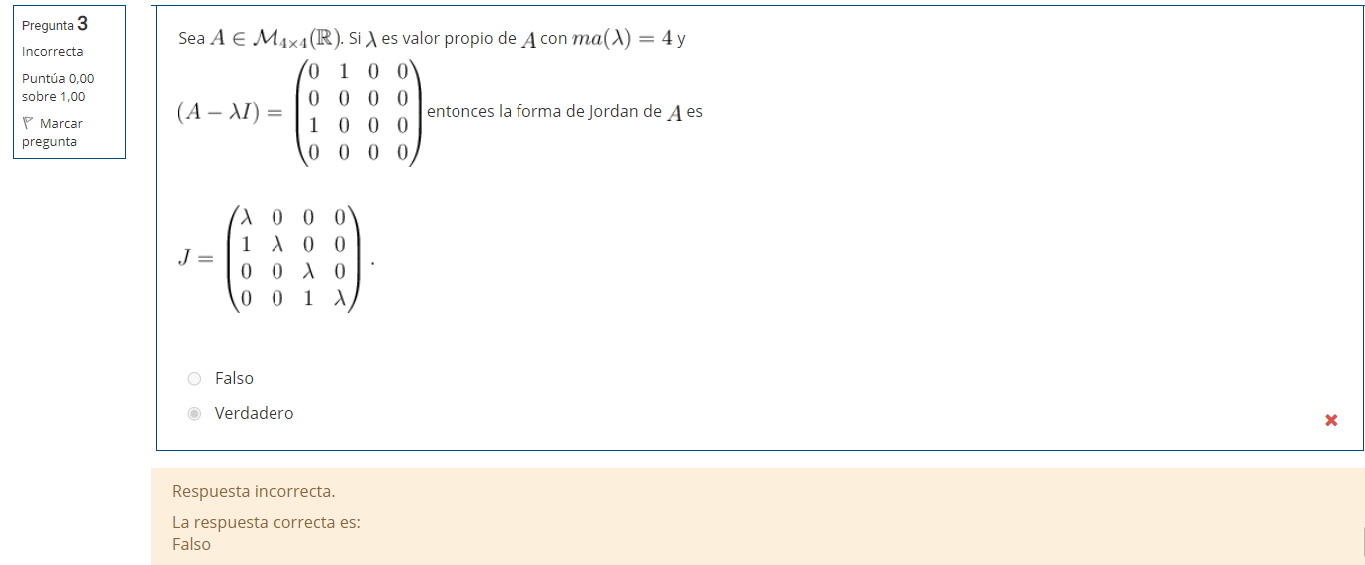
No logro darme cuenta porqué la respuesta a esta pregunta del cuestionario es falso. Agradezco la ayuda.
Hola,
La idea es que como el mayor subbloque (con λ ) en la forma de Jordan J es de tamaño 2 (en este caso, los 2 tienen el mismo tamaño), todos los vectores de una base de Jordan estarían en el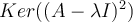
(porque si J es la matriz asociada a T en la base de Jordan 
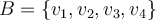el primer subb-bloque te dice que 
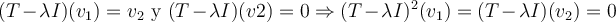y lo mismo para el 2do subbloque.
La idea es que como el mayor subbloque (con λ ) en la forma de Jordan J es de tamaño 2 (en este caso, los 2 tienen el mismo tamaño), todos los vectores de una base de Jordan estarían en el
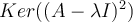(porque si J es la matriz asociada a T en la base de Jordan 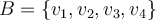el primer subb-bloque te dice que 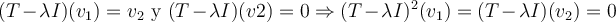y lo mismo para el 2do subbloque.Pero si la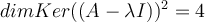 
entonces 
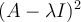tiene que ser la matriz nula, (hay que hacer el cuadrado y ver si es o no la nula)
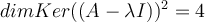entonces 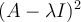tiene que ser la matriz nula, (hay que hacer el cuadrado y ver si es o no la nula)Sigo a las órdenes si no se entendió
Saludos
Marianita
Pero se puede saber a priori como es la forma de Jordan en este caso? Porque como es de tamaño 4, puede ser que un sub bloque sea de tamaño 3, y otro de tamaño 1 también no?
Si, se puede.
Como decís vos, como mg(λ)= dim(Ker(A-λI))=2, la forma de Jordan tiene 2 sub-bloques para el valor propio λ, y como MA( λ)=4, hay dos posibilidades para los tamaños de estos sub-bloques: 3 y 1 o 2 y 2
Ahora como
# {sub-bloques de tamaño ≥ 2} = dim Ker( (A- λI)2 ) - dim(Ker(A-λI)) (*)
Si (A- λI)2 = 0 => # {sub-bloques de tamaño ≥ 2}= 4-2=2 y entonces los tamaños son 2 y 2
Si (A- λI)2 ≠ 0 => # {sub-bloques de tamaño ≥ 2}= 3-2=1 y entonces los tamaños son 3 y 1
Saludos
Marianita
(*) Esto está explicado en mis videos, en las apuntes de Ana y en algunos videos o apuntes con resoluciones de ejercicios.
Como decís vos, como mg(λ)= dim(Ker(A-λI))=2, la forma de Jordan tiene 2 sub-bloques para el valor propio λ, y como MA( λ)=4, hay dos posibilidades para los tamaños de estos sub-bloques: 3 y 1 o 2 y 2
Ahora como
# {sub-bloques de tamaño ≥ 2} = dim Ker( (A- λI)2 ) - dim(Ker(A-λI)) (*)
Si (A- λI)2 = 0 => # {sub-bloques de tamaño ≥ 2}= 4-2=2 y entonces los tamaños son 2 y 2
Si (A- λI)2 ≠ 0 => # {sub-bloques de tamaño ≥ 2}= 3-2=1 y entonces los tamaños son 3 y 1
Saludos
Marianita
(*) Esto está explicado en mis videos, en las apuntes de Ana y en algunos videos o apuntes con resoluciones de ejercicios.