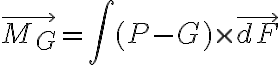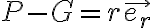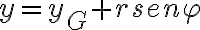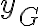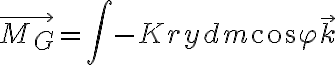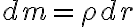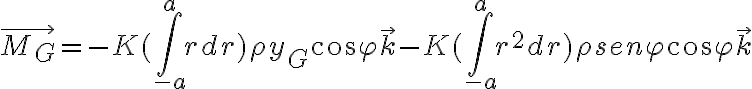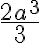Hola ,tengo un problema para calcular el momento angular desde G, no entiendo órque no me queda, y en la solución aparece como que phi punto punto es =-kcos(phi)sen(phi)
Estimada:
El momento en G de la fuerza externa se puede escribir como una integral sobre los elementos de fuerza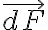 (que da la letra) que se hacen sobre los elementos diferenciales de masa dm que forman la barra como:
(que da la letra) que se hacen sobre los elementos diferenciales de masa dm que forman la barra como:
El momento en G de la fuerza externa se puede escribir como una integral sobre los elementos de fuerza
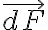 (que da la letra) que se hacen sobre los elementos diferenciales de masa dm que forman la barra como:
(que da la letra) que se hacen sobre los elementos diferenciales de masa dm que forman la barra como: donde P es la posición del elemento diferencial de masa dm. Eligiendo una coordenada r medida sobre la barra a partir del centro de masa (que varía desde - a a a, para recorrer toda la barra), y un versor 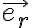 según la dirección de la barra (que forma un ángulo
según la dirección de la barra (que forma un ángulo 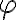 con la recta fija):
con la recta fija):
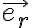 según la dirección de la barra (que forma un ángulo
según la dirección de la barra (que forma un ángulo 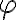 con la recta fija):
con la recta fija): donde 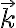 es un versor saliente perpendicular a la mesa horizontal fija. El diferencial de masa lo puedo escribir como:
es un versor saliente perpendicular a la mesa horizontal fija. El diferencial de masa lo puedo escribir como:
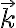 es un versor saliente perpendicular a la mesa horizontal fija. El diferencial de masa lo puedo escribir como:
es un versor saliente perpendicular a la mesa horizontal fija. El diferencial de masa lo puedo escribir como: donde  es la densidad lineal de masa de la barra. Luego expresando el momento como una integral en r:
es la densidad lineal de masa de la barra. Luego expresando el momento como una integral en r:
 es la densidad lineal de masa de la barra. Luego expresando el momento como una integral en r:
es la densidad lineal de masa de la barra. Luego expresando el momento como una integral en r: Saludos:
Ricardo.