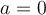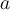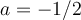Hola, buenas noches, tengo una consulta respecto al siguiente ejercicio:
Mi duda es por qué no sería correcto decir que A es diagonalizable para todo a.
En este ejercicio hallé el polinomio característico y obtuve que los valores propios son a-1, -a-1 y a. Si a es distinto de 0, tenemos 3 valores propios distintos y por lo tanto es diagonalizable. Si a=0, tenemos -1 y 0 como valores propios. Sin embargo, calculé el subespacio S-1 y obtuve que la multiplicidad geometrica de -1 es 2, por lo tanto deduje que A es diagonalizable aunque a=0.
Ese fue mi razonamiento y no logro entender dónde está mi error (Espero que no sea una pavada jeje).
