14.2

14.2

de Nataly Melanie Ruber Maimo -
Número de respuestas: 6

hola en el 14.2 llegué a algo que no tiene mucho sentido, estaba buscando s per y ta me dio esto :/


En respuesta a Nataly Melanie Ruber Maimo

Re: 14.2

de Ana González -
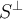Hola Nataly, el error está en suponer que los elementos de S^\perp deben ser polinomios de grado menor o igual a dos. Deberías tomar un polinomio genérico de grado 3 y resolver, siguiendo el razonamiento que hiciste. Con el cuidado de escribir luego al subespacio correctamente. Es decir, por tu razonamiento estas diciendo que 2=-3c, entonces deberías concluir que 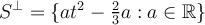S^\perp=\{at^2-\frac{2}{3}a: a\in\mathbb{R}\}. Te lo digo para que cuando corrijas el ejercicio también tengas en cuenta este error.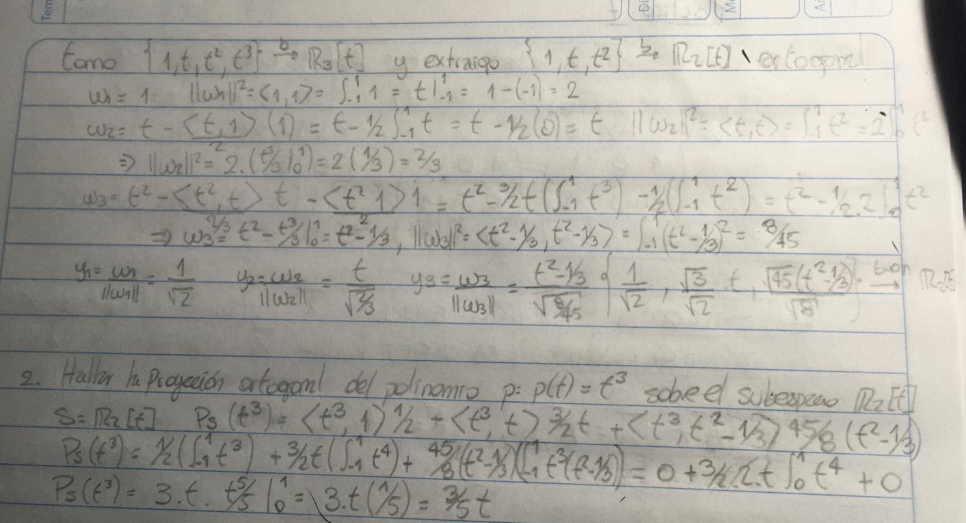
Espero esto aclare la duda.
Saludos
En respuesta a Ana González

Re: 14.2

de Favio Rafael Cardoso Sanchez -
Hola, vengo a plantear la solución a la que llegué


En respuesta a Favio Rafael Cardoso Sanchez

Re: 14.2

de Mariana Pereira -
Hola a todos
La solución que escribió Favio está bien (salvo que en algún momento el -1 en el límite inferior de la integral se le convirtió en un 0, je).
Lo que utilizó para resolverlo es que si B={s1, s2, s3} es una BON de S, entonces 
PS(v)= <v, s1> s1 + <v,s2> s2+ <v,s3>s3 y usó B la bon que obtuvo en la parte anterior
B= \left\{ \frac{1}{\sqrt{2}}, \, \frac{\sqrt{3}}{\sqrt{2}}t,\, \frac{\sqrt{45}}{\sqrt{8}}(t^2-1/3) \right\}

Daniel:
Lo que escribió Ana fue porque Nataly primero quiso hallar S^{\perp}, para después intentar escribir 
t3 como t3  = s+u con s en S, y u en Sperp  . Si hacía eso, entonces s= PS ( t3 ).
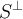Entonces, en el planteo para hallar los elementos u de  S^{\perp}, debería haber tomado u= polinomio genérico de grado 3 tal que 0=<u,1>=<u, t>= <u, t2 >.
Este procedimiento es siguiendo al pie de la letra la primer definición de PS (v). Pero de esta manera para hallar s=PS(v),  tenés que hacerlo hallando también el u tal que v= s+u, y para hallar el u tenés que antes hallar explícitamente  Sperp . Pero al final no importa quién es explícitamente el u.

Entonces podés obviar hallar el u, planteando que buscás un s en S tal que v-s esté en Sperp . Y en ese caso es como decías vos, tomás s= polinomio genérico de grado 2 y hallás los coeficientes planteando que t3-s sea ortogonal a 1, t y a t2 .

Espero que con eso se aclare la cosa
Saludos
Marianita
En respuesta a Mariana Pereira

Re: 14.2

de Favio Rafael Cardoso Sanchez -
Ahí va gracias profe, lo que usé en la integral, viene de la interpretación grafica, porque la integral al ser el área bajo la curva de una función par, es lo mismo calcularla entre -1 y 1 a hacerlo entre 0 y 1 y multiplicarlo por 2.
Gracias por su respuesta!
En respuesta a Favio Rafael Cardoso Sanchez

Re: 14.2

de Mariana Pereira -
Ah, perfecto! No había visto el 2 multiplicando. Sin seguir las cuentas, vi que te diobien entonces cuando vi el 0 pensé que había sido un despiste al pasarlo en limpio.
Disculpas!
Saludos!
Marianita