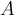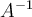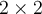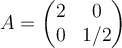GAL2-1S: Consulta ejercicio matriz y su inversa semejante a diagonal

Buenas noches,
Tengo una duda sobre el siguiente ejercicio y hace horas que lo estoy trabajando pero no lo logro resolver.

Yo lo encaro con la definición de semejanza, entonces A = P^-1*D*P y A^-1=R^-1*D*P. Con eso opero e igualo y llego a P*A*P^-1 = Q*A*Q^-1, pero de ahí no se como seguir.
También intente usando la propiedad transitiva de la semejanza, entonces A~D~A^-1 => A~A^-1 y Googleando por esa relación llegue a que la única manera en que se cumpla la relación es que A sea una matriz diagonal con 1 o -1 como valores. Si opero con esa premisa llego enseguida a un contraejemplo de la propuesta pero sinceramente no lo relaciono con algún teorema o propiedad que hallamos visto en el curso.
Por favor, ¿podrían explicarme como sería la forma correcta de encararlo?
Muchas gracias!

Re: Consulta ejercicio matriz y su inversa semejante a diagonal

de Jose Vivero - martes, 11 de mayo de 2021, 14:50

Hola Juan

Conviene recordar que si una matriz cuadrada cualquiera es semejante a la identidad, entonces tiene que ser igual a la identidad. Si el enunciado fuese cierto implicaría que cualquier matriz invertible

$A$ que cumpla que tanto

$A$ como

$A^{-1}$ son semejantes a alguna matriz diagonal tendría que ser la identidad...

Vamos al caso de matrices de tamaño

$2\times 2$ . Sea

$A=\begin{pmatrix} 2 & 0 \\ 0 & 1/2\end{pmatrix}$ , entonces

$A^{-1}=\begin{pmatrix} 1/2 & 0 \\ 0 & 2\end{pmatrix}$ . Puedes encontrar una matriz diagonal semejante a esas dos, pero que no sea la identidad?? Ahí tenés el contraejemplo.

Pensalo y si te persiste todavía alguna duda quedo a las órdenes.

Saludos.

Re: Consulta ejercicio matriz y su inversa semejante a diagonal

de Mariana Pereira - miércoles, 12 de mayo de 2021, 17:52

Hola, lo que obtuviste no es cierto. Puede pasar que A~A^-1 y que A no sea ni diagonal, e incluso siendo diagonal puede tener otros valores a parte de 1 y -1 en la diagonal.
Siguiendo un poco la idea de lo que habías arrancado a pensar:

Fijate que si A = P^-1*D*P entonces inviertiendo a ambos lados obtenés que

A^-1= ( P^-1*D*P )^-1 = P^-1 D^-1 (P^-1)^-1= P^-1D^-1P.
Es decir que en general si A es invertible y A~D entonces A^-1 ~D^-1

Y si D es diagonal, su inversa también es diagonal y en cada lugar de la diagonal tiene el inverso de la correspondiente entrada de D;

Ahora como A^-1 ~D^-1 la diagonal de D^-1 está formada por los valores propios de A^-1 (contando multiplicidades)

Si ADEMÁS A^--1 también es semejante a D, entonces la diagonal de D también está formada por los valores propios de A^-1.

Así que cuando invertís todas las entradas diagonales de D tenés que volver a obtener todas las entradas de D:

Por eso el ejemplo que te puso José, en la diagonal tiene 2 y 1/2