Una pregunta, en este ejercicio: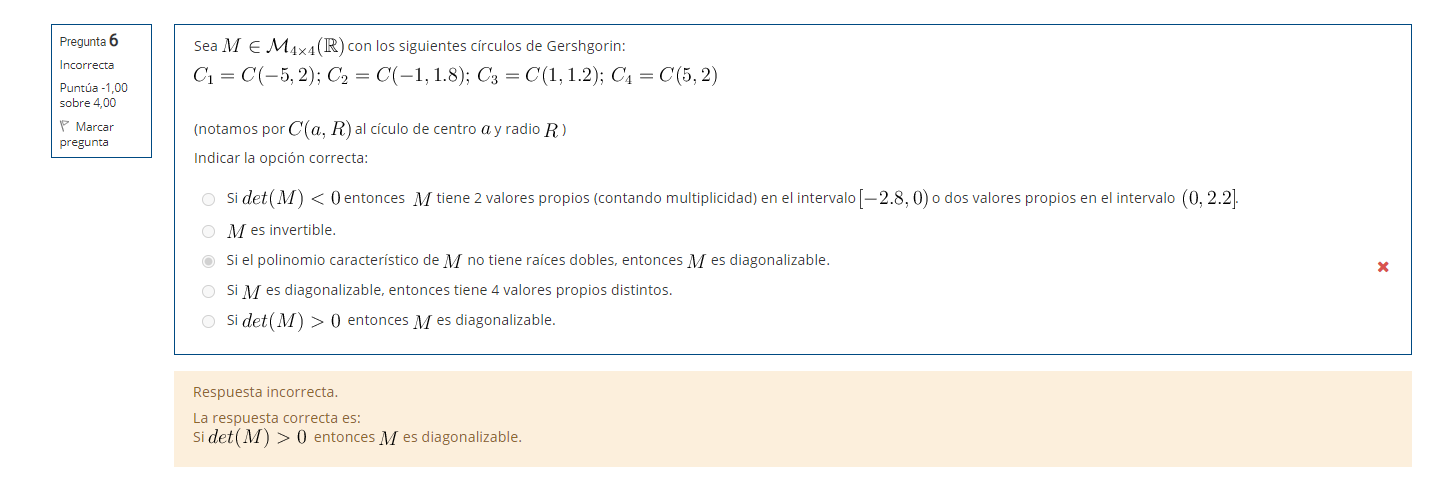
¿Qué te asegura que por tener determinante positivo, todas las raíces del polinomio característico sean reales?
¿No podría ser que tuviese soluciones complejas y por lo tanto no ser diagonalizable?
Una pregunta, en este ejercicio:
¿Qué te asegura que por tener determinante positivo, todas las raíces del polinomio característico sean reales?
¿No podría ser que tuviese soluciones complejas y por lo tanto no ser diagonalizable?
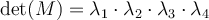 . Como en cada uno de los círculos
. Como en cada uno de los círculos 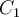 y
y 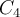 hay un solo valor propio, tiene que ser un número real en ambos casos (¿puedes justificar esto?). Luego hay dos valores propios que son reales, además uno de ellos es negativo y el otro positivo. Eso significa que los dos valores propios que quedan
hay un solo valor propio, tiene que ser un número real en ambos casos (¿puedes justificar esto?). Luego hay dos valores propios que son reales, además uno de ellos es negativo y el otro positivo. Eso significa que los dos valores propios que quedan 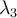 y
y 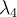 tienen que satisfacer que
tienen que satisfacer que  es un número real negativo. Intenta ahora concluir que la única manera en la que eso es posible es que ambos sean reales (tengan parte imaginaria nula) y además tengan distinto signo.
es un número real negativo. Intenta ahora concluir que la única manera en la que eso es posible es que ambos sean reales (tengan parte imaginaria nula) y además tengan distinto signo. 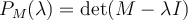 , luego el determinante de M es igual a
, luego el determinante de M es igual a 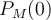 . Por el Teorema Fundamental del álgebra todo polinomio con coeficientes reales se descompone en factores lineales en el cuerpo de los complejos. Luego
. Por el Teorema Fundamental del álgebra todo polinomio con coeficientes reales se descompone en factores lineales en el cuerpo de los complejos. Luego 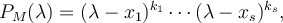 donde los
donde los 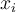 son los valores propios. De aquí que
son los valores propios. De aquí que 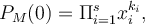 por tanto el determinante es el producto de los valores propios contando las multiplicidades. Ojo que algunos de los
por tanto el determinante es el producto de los valores propios contando las multiplicidades. Ojo que algunos de los 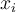 pueden ser complejos, pero como el polinomio tiene coeficientes reales vienen en pares conjugados por tanto esa productoria es siempre un número real.
pueden ser complejos, pero como el polinomio tiene coeficientes reales vienen en pares conjugados por tanto esa productoria es siempre un número real.